Rules of Linear Inequality-Addition, Subtraction, And, Multiplication
The four (4) types of operations that are done on linear inequalities are multiplication, division and addition, and subtraction. The same solution to Linear inequalities is called equivalent inequality. There are rules for both equality and inequality. All the rules explained with the example mentioned below are also true for inequalities involving less than or equal to (≤), and greater than or equal to (≥). Before learning how to solve linear inequalities, the important rules of linear inequality for all these operations.
Addition rules of linear inequality
As per the addition rule of linear inequalities, adding the same number to both sides of the inequality result an equivalent inequality that is the inequality symbol does not change.
If x > y, then x + a > y + a and if x < y, then x + a < y + a
For example: If x > y, then x + a > y + a
Solution:
Let x=5 and y=3
5>3
Adding the same number to both sides
5+2>3+2
7>5
.
- if x < y, then x + a < y + a
let x=4 and y=6
4< 6
Adding the same number to both sides
4+3<6+3
7<9
Hence proved the inequality symbol does not change
Subtraction rules of linear inequalities:
As per the subtraction rule of linear inequalities, subtracting the same number from both sides of the inequality produces an equivalent inequality, which is the inequality symbol does not change.
If x > y, then x − a > y − a and if x < y, then x − a < y − a.
For example: If x > y, then x − a > y – a
Solution:
Let x=7 and y =5
7>5
Subtracting the same number from both sides
7-3>5-3
4>2
- if x < y, then x − a < y – a
Solution:
Let x=5 and y=8
5 <8
Subtracting the same number from both sides.
5-1<8-1
4<7
Hence proved the inequality symbol does not change
Multiplication rule of linear inequality
In the multiplication rule of linear inequalities, multiplication on both sides of an inequality with a positive number same always results in an equivalent inequality that is the inequality symbol does not change.
If x > y and a greater than zero (a > 0),
Then x × a > y × a and if x < y and a > 0,
Then x × a < y × a, Here, × is the multiplication symbol.
For example: If x > y and a > 0 Then x × a > y × a
Solution:
If x > y and a > 0
Let x=3 and y=2 ,a=5
3>2 a > 0
Multiplication on both sides positive number 5
3×5>2×5
15>10
- if x < y and a > 0 Then x × a < y × a
Solution:
Let x=5 and y=7 , a is a positive number 4
x < y and a > 0
5<7
Multiplication on both sides positive number 4
5×4<7×4
20<28
Hence proved: that multiplication on both sides of an inequality with a positive same number always results in an equivalent inequality that is the inequality symbol does not change.
In other words, multiplication on both sides of the inequality with the same negative number does not produce an equivalent. inequality if the inequality symbol is reversed.
If x > y and a < 0, then x × a < y × a and
If x < y and a < 0, then x × a > y × a.
For example: If x > y and a < 0, then x × a < y × a
Solution:
x > y and a < 0
let x=6 and y=3 , a=negative number
6>3
Multiplication on both sides same negative number – 2
6x-2> 3x-2
-12< -6
- If x < y and a < 0, then x × a > y × a
Solution:
Let x=2 and y=3 ,a is negative number
x < y
2<3
Multiplication on both sides same negative number – 2
2x-2< 3x-2
-4>-6
Hence proved
Division rule of linear inequality
In the division rule of linear inequalities, the division of both sides of an inequality with a positive number results in an equivalent inequality that is the inequality symbol does not change.
- If x > y and a > 0, then (x/a) > (y/a) and
if x < y and a > 0, then (x/a) < (y/a).
For example:
- If x > y and a > 0, then (x/a) > (y/a)
Solution: let x > y and a be greater than zero
X=6 and y=4 a > 0
x > y
6>4
6/2> 4/2
3>2
Hence prove
in another word, the division of both sides of an inequality with a negative number produces an equivalent unless we also reverse the direction of the inequality symbol.
- If x > y and a < 0, then (x/a) < (y/a) and
- if x < y and a < 0, then (x/a) > (y/a)
For example;
x < y and a < 0, then (x/a) > (y/a)
Solution:
x < y and a < 0
x=2 and y=4
and a=-2
x < y
2/-2<4/-2
-1>-2
Hence prove

 written by
written by 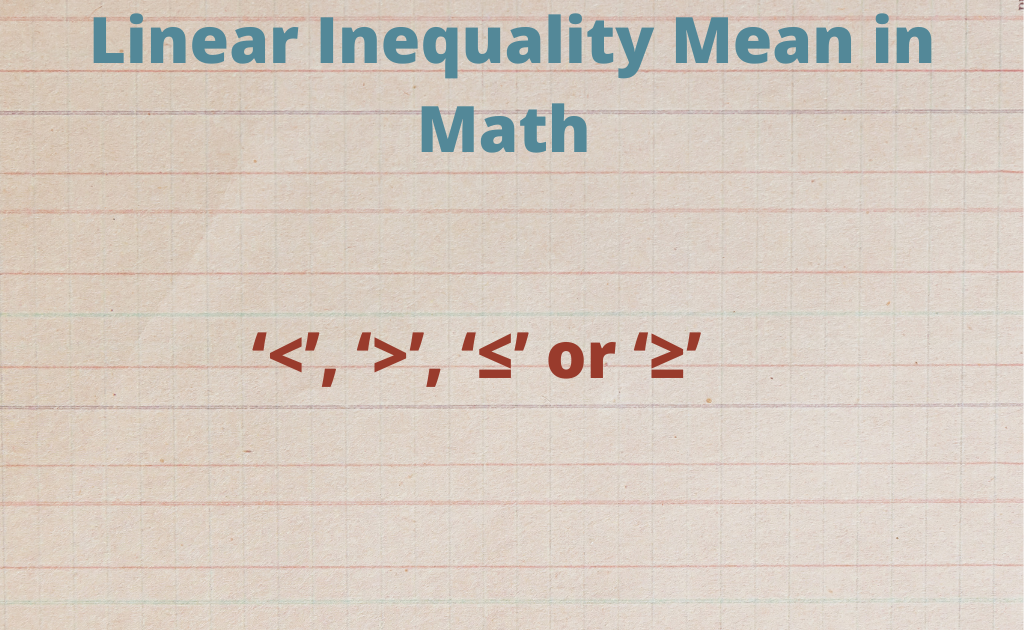


Leave a Reply