Graphing Linear Equations of Two Variables

Graphing linear equations with two variables is an important skill in algebra. It allows us to visualize relationships between two quantities and is a fundamental tool in understanding real-world scenarios.

In this article, we will discuss the graphing linear equations with two variables.

Graphing Linear Equations with Two Variables

Step 1: Identifying the Equation

A linear equation with two variables typically follows the form:

y = mx + b

Here, (m) represents the slope, and (b) is the y-intercept.

Step 2: Plotting the Y-Intercept

Y-intercept (b) is the point where the line crosses the y-axis. To plot it, find the value of (b) and mark that point on the graph.

Step 3: Calculating the Slope

Slope (m) defines the line’s steepness. To find the slope, choose two points on the line and use the formula:

m= y₂ – y₁ / x₂ – x₁

Step 4: Plotting the Line

Starting from the y-intercept, use the calculated slope to find additional points on the line.

Solved Examples

Example

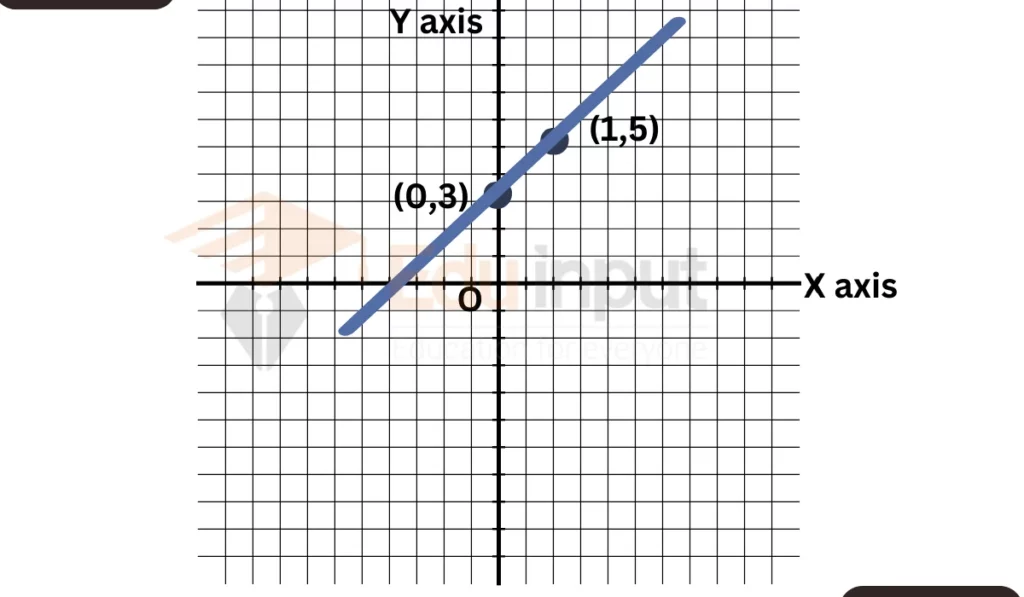
Graph the equation (y = 2x + 3).

Y-Intercept

Put x = 0 in equation,

y = 2(0) + 3

y = 3

So, the first point is (0, 3).

Slope

compare with general equation,

m = 2

Using the slope, we can find another point.

For example, let (x = 1). Then, y = 2(1) + 3 = 5. So, the second point is (1, 5).

Plot the two points on the graph and draw a straight line connecting them.

Example

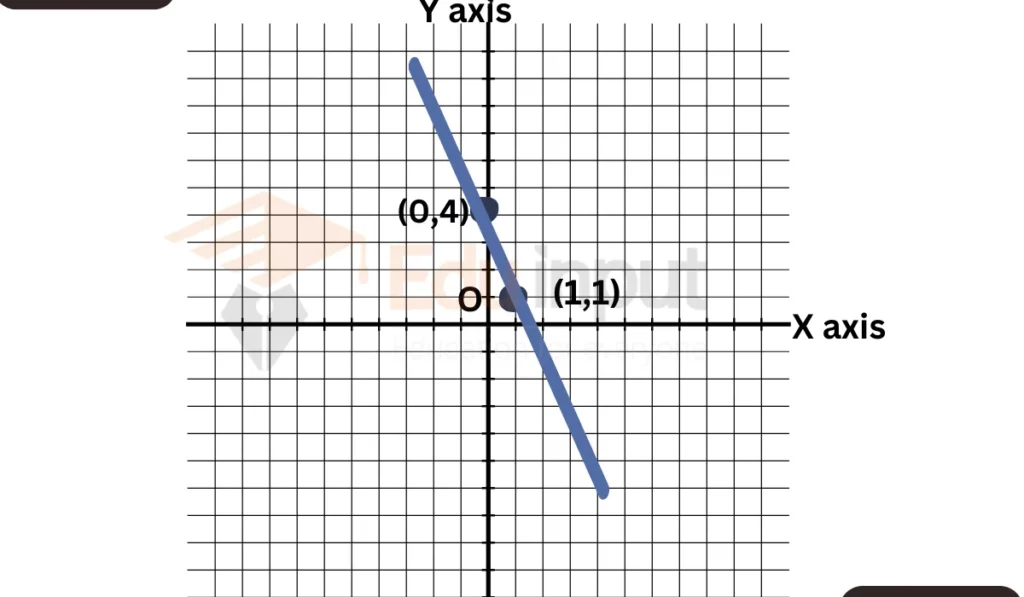
Graph the equation (y = -3x + 4).

Y-Intercept

For Y- intercept, put x=0

y = – 3(0) + 4

y = 4

So, the first point is (0, 4).

Slope

Compare with general equation,

m = -3

Using the slope, we can find another point.

Let (x = 1). Then, (y = -3(1) + 4 = 1). So, the second point is (1, 1).

Plot the points and draw the line.

FAQs