Rational Expressions: Simplification and Operations
Rational expressions are an essential part of algebraic expressions, often used to represent complex fractions. Understanding how to simplify and perform operations on these expressions is an important for solving various mathematical problems.
In this article, we will discuss the basics of rational expressions.
What Are Rational Expressions?
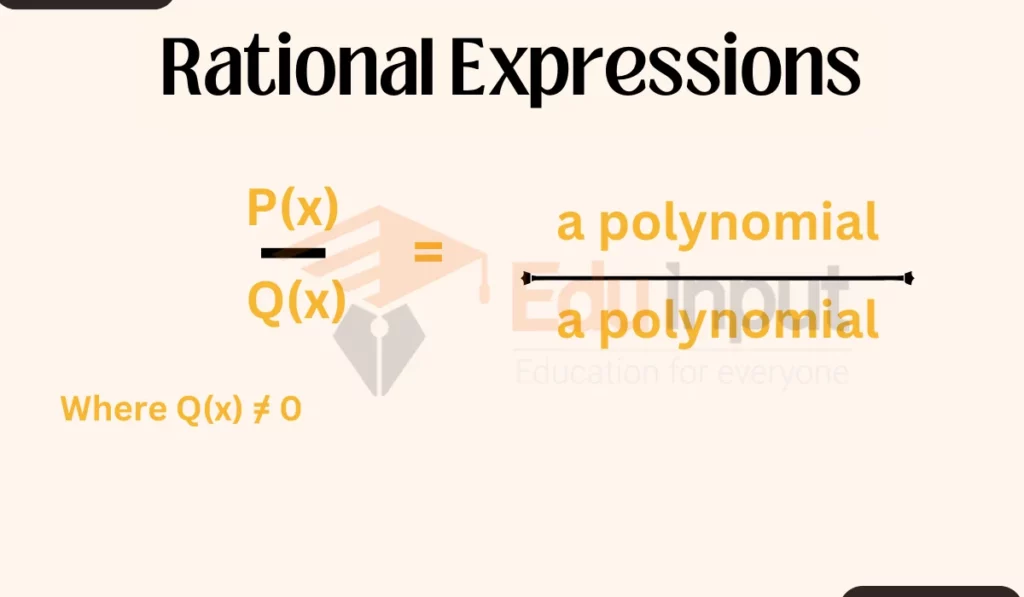
Rational expressions are fractions where both the numerator and the denominator are polynomials.
If f is a rational expression then f can be written in the form p/q where p and q are polynomials.
For example,
Expression (3x + 1)/(2x – 5) is a rational expression because both the numerator (3x + 1) and the denominator (2x – 5) are polynomials.
Simplifying Rational Expressions
1: Factor the Numerator and Denominator
Example
For the expression (4x2 – 9)/(12x2 – 27), factor both the numerator and the denominator:
Numerator: 4x2 – 9 = (2x + 3)(2x – 3)
Denominator: 12x2 – 27 = 3(2x + 3)(2x – 3)
2: Cancel Common Factors
Once you have factored the numerator and denominator, cancel out any common factors.
In above Example, both the numerator and denominator have the factor (2x – 3), so you can cancel it.
(2x + 3)(2x – 3) / [3(2x + 3)(2x – 3)] = 1 / 3
The simplified expression is 1/3.
Operations with Rational Expressions
1: Addition and Subtraction
When adding or subtracting rational expressions, ensure they have a common denominator.
If not, find the least common multiple (LCM) of the denominators and make both fractions have this common denominator.
Example
Add (2/x) + (3/x2).
First, find a common denominator, which is x2 for both fractions. Rewrite them with this common denominator:
(2/x) + (3/x2) = (2x/x2) + (3/x2)
= (2x + 3)/x2
2: Multiplication
To multiply rational expressions, simply multiply the numerators and denominators.
Example
Multiply (x/2) * (4/x2).
x/2 * 4/x2 = 4x / 2x2
= 2/x
3: Division
To divide rational expressions, multiply by the reciprocal of the second expression.
Example
Divide (3/x) by (5/x2).
3/x / 5/x2 = 3/x * x2/5
= 3x/5
The result is (3x/5).
FAQs
What is a rational expression?
A rational expression is a fraction where both the numerator and the denominator are polynomials.
How do I simplify a rational expression?
To simplify a rational expression, factor both the numerator and denominator, and then cancel common factors.
What is the least common multiple (LCM) in rational expressions?
The LCM is the smallest common multiple of the denominators when adding or subtracting rational expressions.
Can I cancel factors in a rational expression?
Yes, you can cancel common factors in the numerator and denominator, just like you would with regular fraction.





Leave a Reply