Integer Factorization

Integers are whole numbers, both positive and negative, including zero. Examples of integers are -3, -2, -1, 0, 1, 2, 3, and so on. Integer factorization is the process of expressing a composite number as the product of its prime factors

In this article, we’ll discuss the concept of integer factorization.

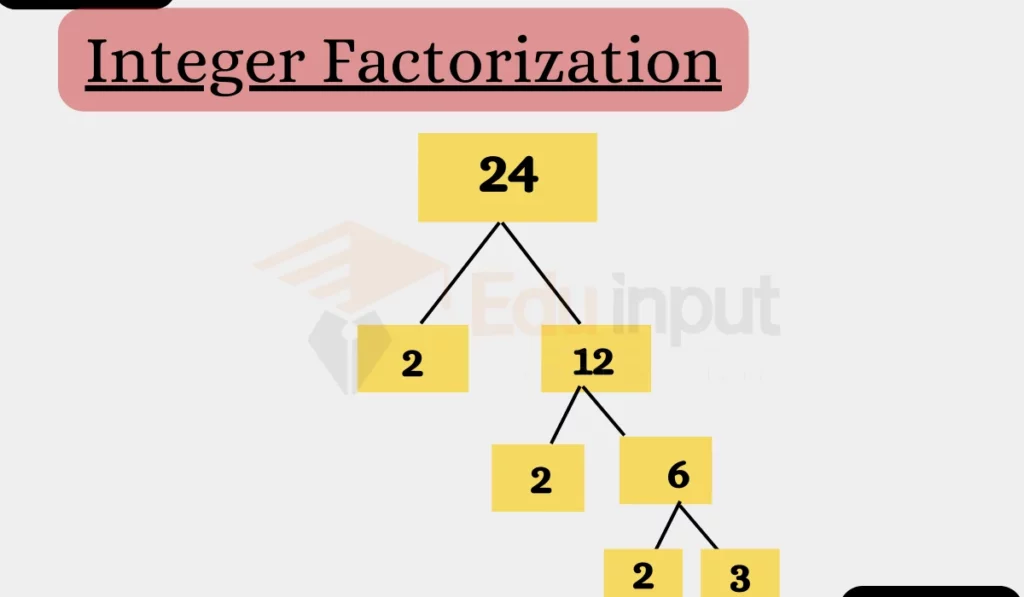
How to Factorize Integers

Step 1: Identify the Integer

Factorize this number 24.

Step 2: Find the Prime Factors

Now, we break down 24 into its prime factors. For 24, the prime factors are 2, 2, 2, and 3.

Step 3: Express as a Product

Combine these prime factors: 2 x 2 x 2 x 3 = 24.

So, the prime factorization of 24 is 2^3 * 3.

Solved Examples

Example

Factorizing 36

Identify the Integer 36

Find the Prime Factors 2, 2, 3, 3

Express as a Product 2 x 2 x 3 x 3 = 36

Therefore, the prime factorization of 36 is 2^2 * 3^2.

Example

Factorizing -48

Identify the Integer (-48)

Find the Prime Factors 2, 2, 2, 2, 3

Express as a Product -1 x 2 x 2 x 2 x 2 x 3 = -48

So, the prime factorization of -48 is -1 x 2^4 x 3.

Also Read:

Tensor Factorization

Factoring Exponentials

FAQs