Simple Harmonic Motion | Hook’s law

Simple harmonic motion is a type of motion where the restoring force on the moving object is directly proportional to the magnitude of displacement and acts toward the object’s equilibrium position.

Simple Harmonic Motion

It is a special kind of vibratory motion that has the following properties.

• Acceleration is proportional to displacement.
• Acceleration is always directed towards the mean position.

 It can be expressed mathematically as follows:

a∝ – x

A body is said to execute simple harmonic motion if its instantaneous acceleration is directly proportional to the displacement and is always directed toward the mean position.

Hook’s law

Let us consider a body of mass m attached to one end of an elastic spring and placed on a frictionless horizontal surface.

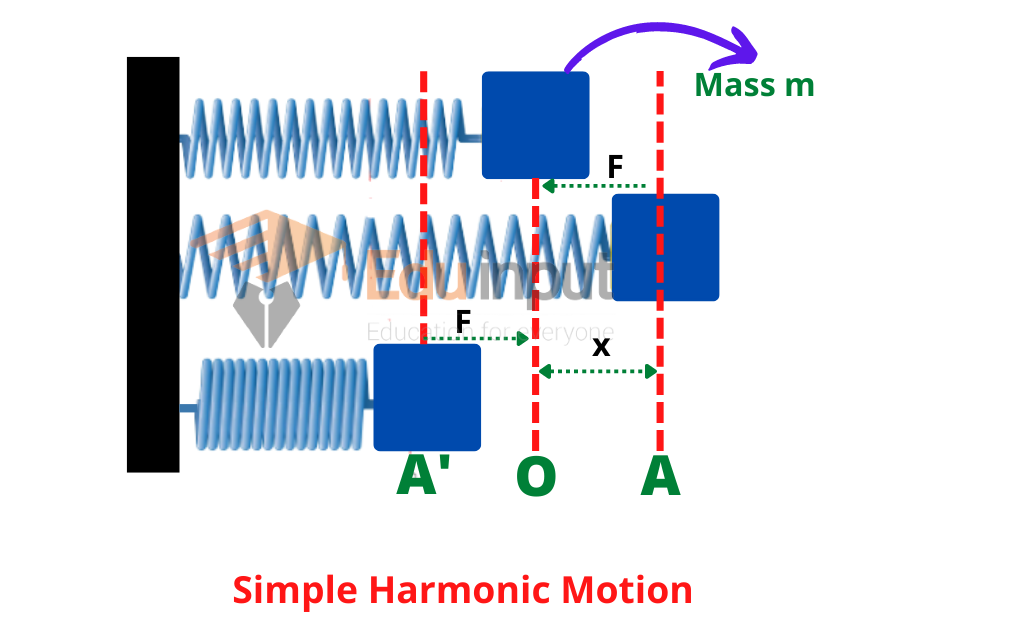
 When the body is pulled toward the right a distance x.The force F according to Hooke’s law is given by

F=kx

Here k is called the spring constant its value depends upon the material of the spring and the length of the spring. Due to elasticity, the spring pulls the body with a force equal in magnitude to the force but opposite in direction. This force is called the restoring force or Hook’s law force and is given by

F = -kx

 The negative sign indicates that F is opposite the x. When the body is released it starts moving towards the mean position and it accelerates with time t passes through the mean position but does not stop there due to inertia and moves towards A and slows down.

Again reaching A it stops and starts moving towards the mean position.

 In this way, it vibrates between the two extreme positions under the action of restoring force and executes the simple harmonic motion. According to Newton’s law of motion

F=ma

ma=-kx

a=-(k/m) x

Since k/m is constant so

a=-constant x

a∝ -x

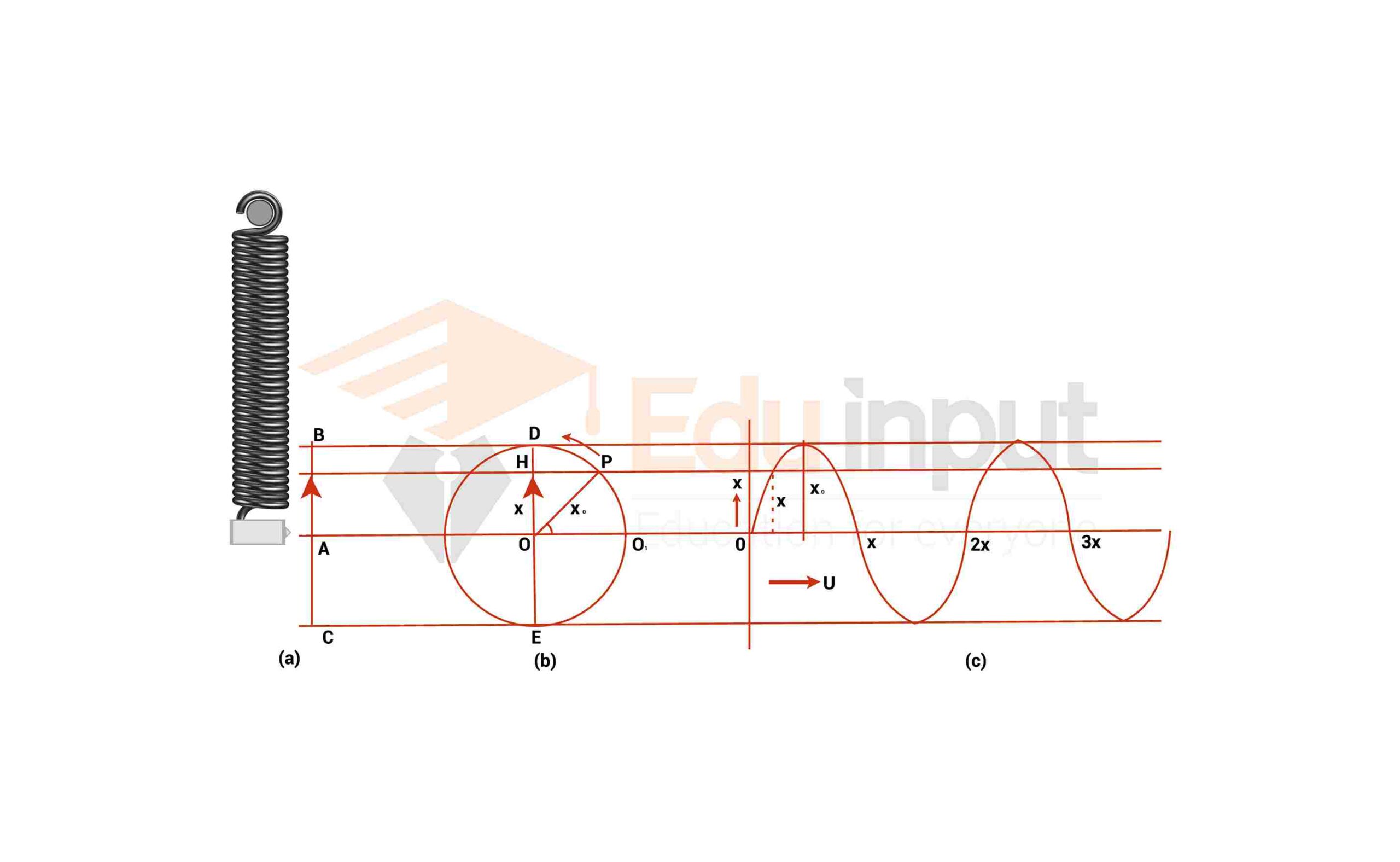
acceleration is proportional to the displacement and is always directed towards the mean position. Now it is clear that the motion of the body is simple harmonic motion. To understand the different parameters of simple harmonic motion Consider a small mass m suspended with a vertical spring.

A sheet of paper is placed behind the mass and there is an arrangement that the paper moves with a constant speed from right to leave a pen is attached to the vibrating mass which just touches the paper and records the displacement against the time.

Instantaneous Displacement and Amplitude of Vibration:

The variation of displacement with time is a sine curve. It is usually known as the waveform of simple harmonic motion. Points B and D correspond to the extreme position of the vibrating mass and points A C and E show its mean position.

Thus the line ACE represents the level of the mean position of the mass on the paper. The amplitude of vibration is thus measured by the line Bb or Dd.

Vibration:

One complete round trip of the body is called vibration (or) the motion of a body from one extreme position to another is called vibration. In the above figure, one vibration will be from B to F or from D to H.

 Time Period (T)

The time required to complete one vibration is called the time period. Its SI units are second (s).

Frequency (F):

 The number of vibrations made in one second is called frequency. Its Si units are hertz (Hz). It is also expressed as vibrations per second or cycles per second. The time period and frequency are related by the equation: T=1/f

 Instantaneous Displacement (x)

The displacement of a body at any instant from the mean position is called instantaneous displacement or simply displacement. It is denoted by x

Amplitude (x_o)

It is the maximum displacement of the body on either side from the mean position. It is denoted by x_o

Angular frequency:

If T is the time period of a body executing simple harmonic motion then its frequency is given by

ω=2π /T

Angular frequency is basically the characteristic of circular motion.