Torque- Definition, Example, And Torque On a Rigid Body

The turning effect of a force produced in a body about an axis of rotation is called Torque.

Torque

A physical quantity that produces an angular acceleration in a body about the axis of rotation is called Torque.  It is the measure of force that rotates an object around an axis.

Example:

When a spanner is used to tighten a nut, torque is produced.

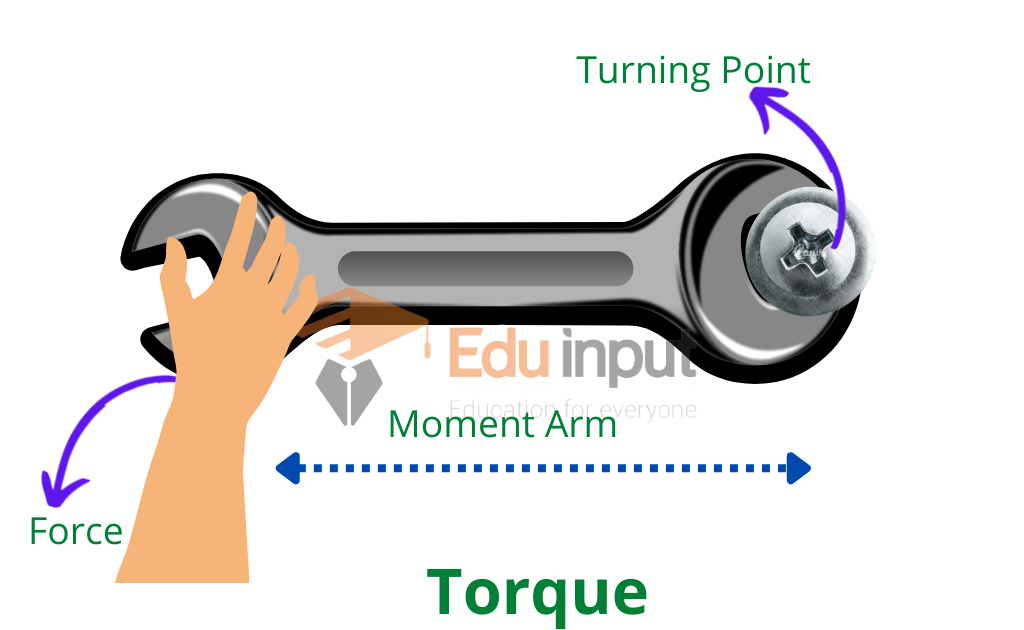
Torque Equation

Torque is the product of force F and Moment arm l. The magnitude of torque is denoted by τ is given by

τ=IF

Unit of torque

The Torque is a vector quantity and the SI unit of torque is Newton meter (Nm).

Dimensions of Torque

The dimensions of torque are:[ML²T²]

Torque Depends on What Factors

The turning effect depends upon two factors

1) Force     2) Moment arm

• Thus if the applied force is increased then more torque is produced.
• If the length of the spanner is longer the turning effect is greater.

Line of Action of the Force

 The direction in which a force act is called the force’s line of action.

Moment Arm

The perpendicular distance between the line of action of force and the axis of rotation is called the moment arm.

If the line of action of the applied force passes through the axis of rotation then moment arm l=0

τ =1xF=IF sin 90°

So

        τ =0xF

         τ =0

Torque on a Rigid Body

If the distance between any two points of a body remains constant by applying a force then such a body is called a rigid body.

Let a force F is acting on a rigid body at point P whose position vector relative to pivot O is r.

The force F can be resolved into two rectangular components.

• F Sin θ perpendicular to r
• F Cos θ along the direction of r

Since the angle between r and F Cos & is zero so torque due to F Cos will be zero. The torque due to F is produced only along F sin θ about 0. It is given by,

    τ = (f sin θ) r=r f sin θ

Alternatively, the moment arm l is equal to the magnitude of the component of r perpendicular to the line of action of F, then

τ =(r sin θ) f    =r f sin θ

Where ‘ θ ‘ is the angle between r and f

the torque can be defined by the vector product of position vector r and the force F

τ =r × f

τ=(r f sin θ) n

Direction of torque

In equation τ=(r f sin θ) n,r F Sin θ gives the magnitude of the torque and n gives the direction of the torque. The right-hand rule determines the direction of torque.

Right-hand rule for torque

According to this rule, the direction of the torque is perpendicular to the plane containing r and F. Anti-clockwise torque is taken as positive and clockwise torque is taken as negative.

Torque and angular acceleration:

As force determines the linear acceleration in a body, similarly torque determines the angular acceleration in a body.

 Torque is the counterpart of force for rotational motion. If a body is at rest or moving with uniform angular velocity, then the angular acceleration is zero and as a result, torque acting on the body is also zero.

Related FAQs