10 Examples of Y-Intercept

Y-intercept is an important idea in mathematics. It’s the point where a line or curve touches the up-and-down line (y-axis) on a graph.

In this article, we will discuss ten examples of y-intercepts in mathematic

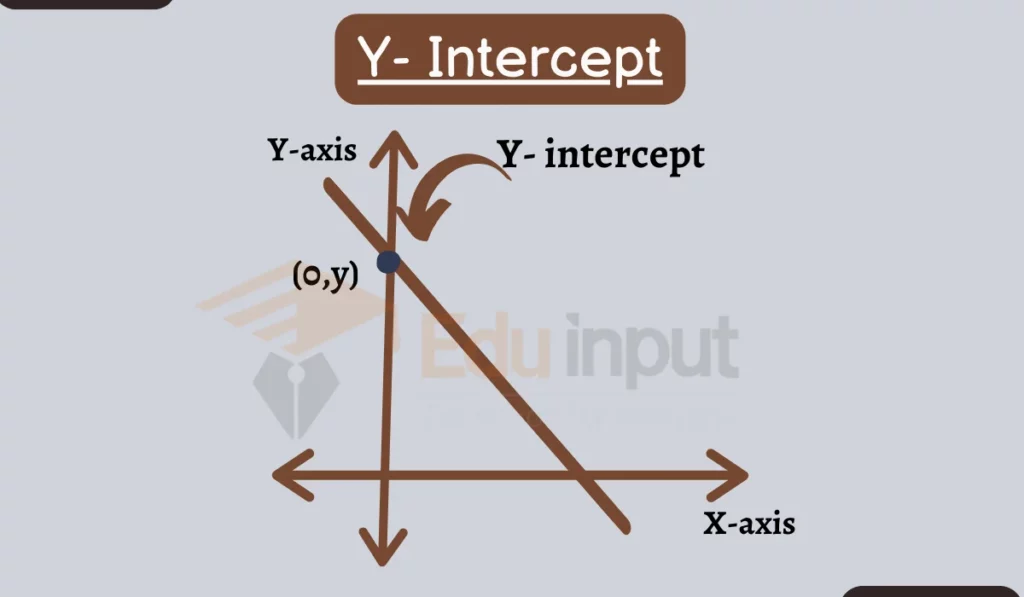
Examples of Y-Intercept

These are 10 examples of y-intercept.

1: Linear Equation

Example

Find the y-intercept of the linear equation y = 3x + 2.

Solution

In this equation, the y-intercept occurs when x is 0. Substitute x = 0 into the equation: y = 3(0) + 2 = 2. So, the y-intercept is 2.

2: Graphing a Line

Example

Given the equation y = -2x + 5, graph the line and find the y-intercept.

Solution

To find the y-intercept, set x to 0: y = -2(0) + 5 = 5. The y-intercept is (0, 5).

3: Quadratic Equation

Example

Determine the y-intercept of the quadratic equation y = x^2 – 4x – 5.

Solution

To find the y-intercept, set x to 0: y = (0)^2 – 4(0) – 5 = -5. The y-intercept is -5.

4: Slope-Intercept Form

Example

Given the equation y = 2x – 3, identify the slope and y-intercept.

Solution

Slope is the coefficient of x, which is 2. The y-intercept is the constant term, which is -3.

5: Parallel Lines

Example

If a line is parallel to another line with a y-intercept of (0, 4), what is its y-intercept if the slope is -2?

Solution

Y-intercept remains the same as the original line, so it is (0, 4).

6: Absolute Value Function

Example

For the absolute value function y = |x| – 1, find the y-intercept.

Solution

Set x to 0: y = |0| – 1 = 0 – 1 = -1. The y-intercept is (0, -1).

7: Horizontal Line

Example

Determine the y-intercept of the horizontal line with the equation y = 7.

Solution

Y-intercept is the point where the line crosses the y-axis, which is (0, 7).

8: Exponential Function

Example

For the exponential function y = 2^x, what is the y-intercept?

Solution

Set x to 0: y = 2^0 = 1. The y-intercept is (0, 1).

9: Cubic Equation

Example

Calculate the y-intercept of the cubic equation y = x^3 – 6x^2 + 11x – 6.

Solution

Set x to 0: y = (0)^3 – 6(0)^2 + 11(0) – 6 = -6. The y-intercept is -6.

10: Vertical Line

Example

Determine the y-intercept of a vertical line that has the equation x = -3.

Solution

Vertical lines do not have y-intercepts as they are parallel to the y-axis.