Factoring Polynomials: Techniques and Examples
Factoring polynomials is a fundamental skill in algebra. It helps us simplify tricky math problems by breaking them into smaller, manageable parts.
In this article, we’ll discuss different ways to do factoring polynomials.
What is Factoring a Polynomial?
Factoring a polynomial means finding its factors, which are expressions that, when multiplied together, yield the original polynomial. It is the reverse process of multiplication.
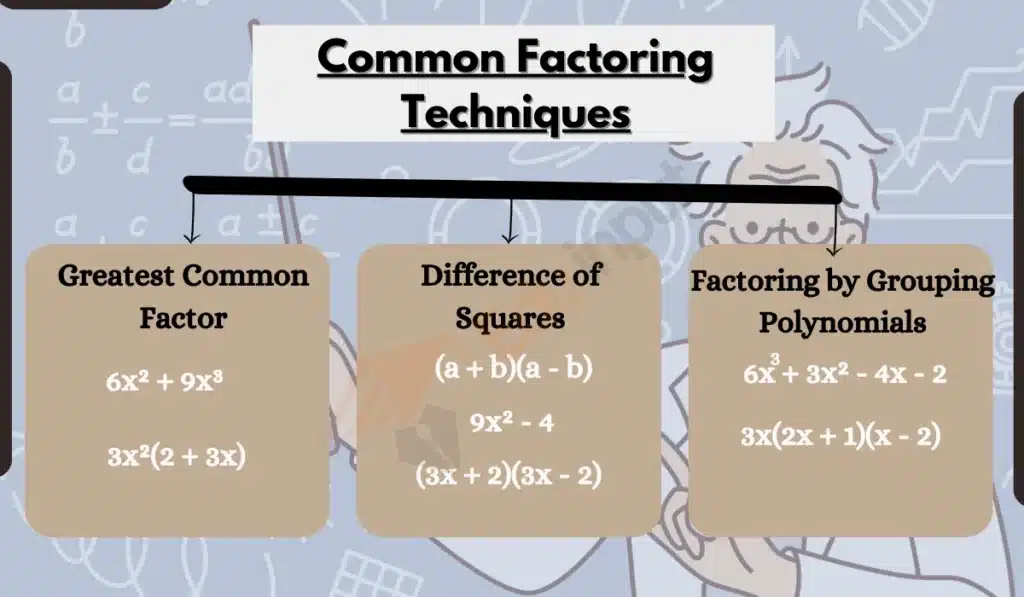
Common Factoring Techniques
1: Greatest Common Factor (GCF)
Often, a polynomial has a common factor in all its terms. To factor this out, follow these steps:
- Identify the greatest common factor (GCF) of all the terms in the polynomial.
- Divide each term by the GCF.
- Express the polynomial as the product of the GCF and the simplified expression.
Example
Factoring the GCF of 6x² + 9x³:
Step 1: GCF of 6x² and 9x³ is 3x².
Step 2: Divide each term by 3x²:
6x²/3x² + 9x³/3x² = 2 + 3x
Step 3: The factored polynomial is 3x²(2 + 3x).
2: Factor by Grouping
Factor by grouping method works for polynomials with four terms. You group the first two terms and last two terms, factor each group, and then factor out the common factor:
Example
x2 + 5x + 6x + 30
= (x2+ 5x) + (6x + 30)
= x(x + 5) + 6(x + 5)
= (x + 5)(x + 6)
3: Factor Trinomials
Trinomials are polynomials with three terms. To factor a trinomial in the form ax2 + bx + c, follow these steps:
- Find factors of c that add up to b
- Split the middle term bx into the two factors found
- Factor each group
Example
x2+ 7x + 12
Factors of 12 that add to 7 are 3 and 4
Split 7x into 3x + 4x
= x2 + 3x + 4x + 12
= x(x + 3) + 4(x + 3)
= (x + 3)(x + 4)
4: Difference of Squares
Difference of squares occurs when you have a binomial in the form a2 – b2. This can be factored as:
(a + b)(a – b)
Example
9x2 – 4
9x2 – 4 = (3x)2 – 22
Factor as difference of squares:
= (3x + 2)(3x – 2)
5: Factoring by Grouping Polynomials
Factor by grouping method can work for polynomials with more than 4 terms. You group terms together, factor each group, and factor out the common factor.
Example
= 6x3 + 3x2 – 4x – 2
= (6x3 + 3x2) + (-4x – 2)
= 3x(2x2 + x) – 2(2x + 1)
= 3x(2x + 1)(x – 2)
FAQs
How do you know which factoring method to use?
Look at the form of the polynomial. Trinomials can be factored using the factoring trinomial method. Binomials may be a difference of squares. Polynomials with 4 or more terms can try factor by grouping.
What if I can’t factor the polynomial?
If none of the basic factoring methods work, the polynomial may not be factorable. You can use the rational root theorem or synthetic division to check for factors. Some polynomials are prime polynomials and cannot be factored.
What is the best way to get good at factoring polynomials?
Practice! Work through many examples of factoring different types of polynomials. Look for patterns that signal certain factoring methods.





Leave a Reply