Introduction to Algebraic Word Problems
Algebraic word problems are math problems expressed using words rather than just equations and numbers. They require translating the written words into mathematical equations in order to solve them.
In this article we will discuss how to solve the algebraic word problems.
Basic Approach
When starting an algebraic word problem, follow these basic steps:
- Read the entire problem carefully, more than once if necessary, to understand what the problem is asking.
- Identify the key information and quantities given in the problem. Make sure you understand what each quantity represents.
- Define variables to represent unknown values. Typically, a letter like x or y is used.
- Translate the wording into mathematical equations with your defined variables.
- Solve the equations to find the value of the unknowns.
- Answer the question asked in the problem using your solved values.
Types of Algebraic Word Problems
Some common types of algebraic word problems include:
Age problems
These involve determining a person’s age or the amount of time that has elapsed. Equations use variables representing ages and setups like “Tom’s age in 5 years” or “Mary is 2 years older than John.”
Mixture problems
These involve combining two amounts with different values per unit, like solutions mixed at varying concentrations. Equations have terms for the total amount, amounts of each mixture, and concentrations.
Geometry problems
These involve perimeter, area, angles, and other geometric operations. Equations relate the geometric values like the area of a rectangle in terms of its width and length.
Interest problems
These involve calculating interest earned based on principles like simple or compound interest over time. Equations relate interest amounts, rates, principal investments, and time periods.
Divisions and Fractions in Word Problems
Some tips when word problems involve divisions or fractions:
- Use a variable like x to represent a fractional amount or what is being divided.
- Make sure to keep track of the original total amount and what fractions have been taken away.
- For interest and mixture problems with changing amounts over time, isolate each time period with separate variables and equations.
- Multiply both sides of the equation by the denominator to eliminate any fractions in the equations to be solved.
Example Word Problem
Jack and Jill each set aside part of their weekly $10 allowance. Jack put 2/5 of his $10 into savings. Jill put 1/4 of her $10 into savings. How much more money did Jack put into savings than Jill?
Solution
Let x = Jack’s amount put into savings
Let y = Jill’s amount put into savings
Jack put 2/5 of $10 into savings. 2/5 of $10 is (2/5) * $10 = $4.
So, x = $4
Jill put 1/4 of $10 into savings. 1/4 of $10 is (1/4) * $10 = $2.50.
So, y = $2.50
Jack put x – y more into savings than Jill.
x – y = $4 – $2.50 = $1.50
Therefore, the amount Jack put into savings that was $1.50 more than Jill.
FAQs
What are the basic steps for solving any algebraic word problem?
The basic steps are:
Read and understand the problem.
Identify known and unknown quantities.
Define variables to represent unknowns.
Translate the wording into mathematical equations.
Solve the equations.
Answer the original question with the solved values.
What should I do if I get stuck translating a word problem into equations?
Break the problem down into smaller steps and translate just one step at a time. Review examples of similar problems. Try rewording the problem in your own words
When do I combine equations vs isolate them in multi-step word problems?
For processes happening in sequence like accumulating interest, isolate each step in its own equation. For related quantities like width and length, combine the equations into one with multiple variables.
What are some common mistakes when solving algebraic word problems?
Not reading the full problem, making assumptions, or skipping steps in your hurry to get to a solution. Losing track of what each variable represents. Mistakes in the math when translating words to equations.

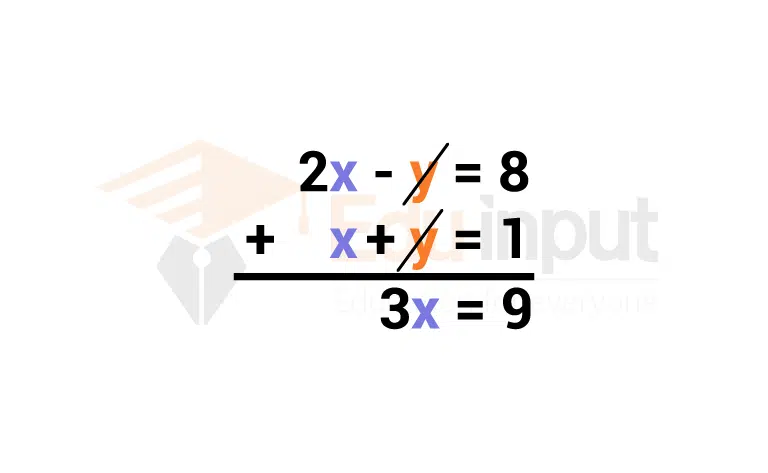



Leave a Reply