Molar Specific Heat-Specific heat, And Types

Specific heat is the heat that requires raising the temperature of a substance by one-kilo gram while molar specific heat is the heat that requires raising the temperature of one mole of a substance.

Specific heat

The amount of heat energy required to raise the temperature of 1 Kg of a substance through 1 K is called Specific Heat. The unit of specific heat is J/g °C

For example, the Specific heat of air is 1.012 J/g °C.

Molar Specific Heat

The amount of heat energy required to raise the temperature of 1 mole of a substance through 1 K is called Molar Specific Heat. Its unit is J/mol °C.

The molar-specific heat of air is 29.19  J/mol °C

One kilogram of different substances contains a different number of molecules. As one mole of any substance contains equal molecules, hence it is better to take mass in moles and the specific heat in molar specific heat.

Types of molar Specific Heat

A gas can be heated in the following two ways

• Constant pressure
• Constant volume

So molar specific heats are also defined in two ways:

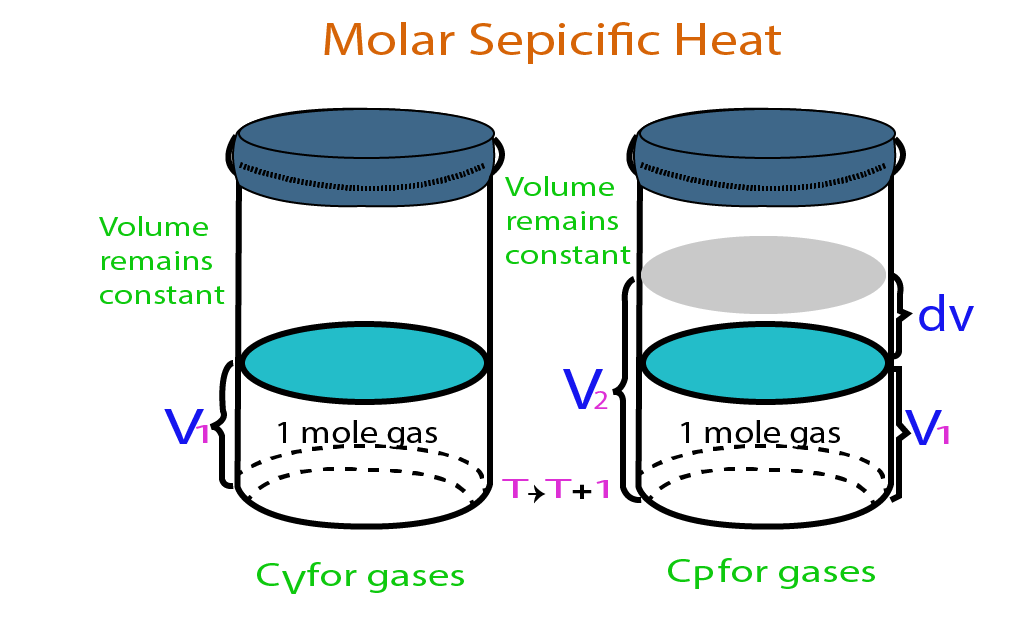
Molar-specific heat at constant pressure:

The amount of heat required to raise the temperature of one mole of the gas through 1 K at constant pressure is called Molar Specific Heat at constant pressure.

It is denoted by C_p.

Molar-specific heat at constant volume

The amount of heat required to raise the temperature of one mole of the gas through 1 K at constant volume is called Molar Specific Heat at constant pressure.

It is denoted by C_v.

DERIVATION OF C_p -C_v =R

Consider one mole of an ideal gas in a cylinder having a fixed piston. The gas is heated at a constant volume. So the heat supplied is used in increasing the temperature only. Here Q is the heat , ΔU is a change in internal energy and W is work done by the heat.

Q=ΔU-W

Q_v=ΔU-PΔV

Q_v=ΔU

Q_v=C_v ΔT

ΔU=C_v ΔT

Now a similar cylinder with a free piston. The gas is heated at constant pressure. In this case, the heat supplied is used in increasing the temperature as well as in doing work for moving the piston up.

Q=ΔU +W

Q_p =ΔU +PΔV

Q_p =C_pΔT

C_pΔT=ΔU +PΔV

But increase in the internal energy at constant pressure is equal to an increase in internal energy at constant volume.

C_pΔT=C_vΔT+PΔV

Using the ideal gas equation for 1 mole n=1

PV=RT

At constant pressure P let the change in volume be ΔV

Due to the rise in temperature ΔT then

PΔV=RΔT

C_pΔT=C_vΔT+ RΔT

C_p=C_v +R

C_p-C_v=R

It is clear from this equation that the molar-specific heat at constant pressure is greater than molar-specific heat at constant volume.