Operations On Matrix | Transpose of a Matrix and Inverse of Matrix

There are 3 main operations on the matrix

• Addition
• Subtraction
• Multiplication

Addition of matrices:

Two matrices A and B can be added if they have the same orders and their corresponding entries are added.

Example:

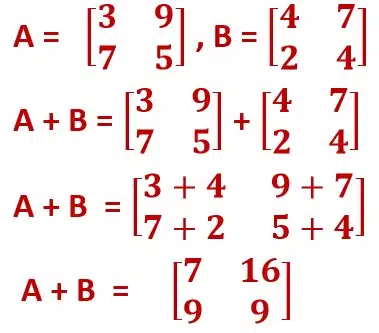
Subtraction of Matrices:

Two matrices A and B can be subtracted if they have the same orders and their corresponding entries are subtracted.

Multiplication of Matrices:

Matrix multiplication or multiplication of matrices is one of the operations that can be performed on matrices in linear algebra.

If A and B are two given matrices then the multiplication of these matrices is possible, if A and B are compatible.

Matrix multiplication is a binary operation, that gives a matrix from two given matrices.

A and B matrices are said to be compatible if the number of columns of the A matrix is equal to the number of rows of matrix B.

Example:

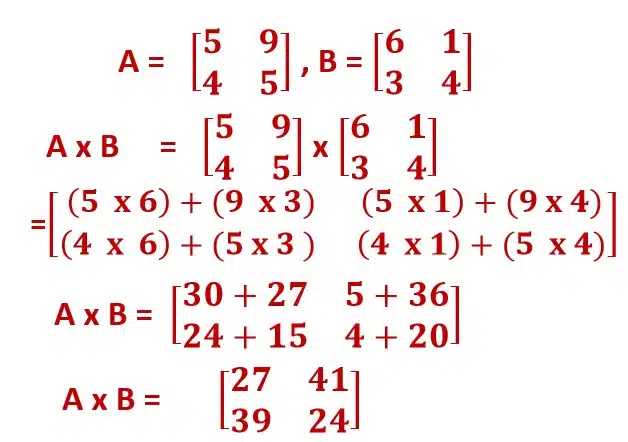
Transpose of the matrix:

The transpose of a matrix is obtained by changing the rows into columns and columns into rows. Transpose of a matrix is denoted by A^t.

For example, if we have a matrix A

In this matrix, there are 3 rows and 3 columns. The rows will convert into columns and columns into rows.

Negative of a matrix:

If we have a matrix A,

Negative of A is obtained by changing the sign of each entry of A. The negative of A is denoted by –A.

Inverse of Matrix:

If we have a matrix A, the inverse of the matrix will be,

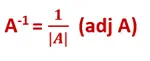
The inverse of the matrix is denoted by A^-1.

Frequently Asked Question-FAQs