Theorems of the Subgroup
Let (G,*) be a group and H be a non-empty subset of G.if H itself is a group with the same binary operation (*).Than H Is called a subgroup of G. In this article we will discuss the Theorems of the Subgroup
Statement: Let (G,.) be a group, then a non
-empty subset H of G is a subgroup if and only if
a,b ∈H imply ab-1 ∈H.
Proof:
Suppose H is a subgroup of G
H itself is a group
So ∀a,b∈H –>a,b-1 ∈H
ab-1 ∈H
∴ H is group
Conversely
Suppose
a,b-1 ∈H —> ab-1 ∈H —> (1)
Here we prove H is the group
Let a∈H
a,a ∈H –>aa-1 ∈H –> eH
by (1)
Identity elements exist in H
e,a∈H –> ea -1∈H –>a-1∈H
by (1)
The inverse of each element exists in H
Let a,b∈H –> a,b-1 ∈H
a(b-1)-1∈H
by (1)
ab∈H
H is closed
Since G is a group
(ab)c=a(bc) ∀ a,b,c∈G
H is a subset of G
Associative law held in H.
By 1,2,3,4
H itself group
Hence proved;
H is a subgroup of G
Statement: The intersection of any collection of subgroups of a group G.is a subgroup of G.
Proof:
Let {Hi , i∈I } be family of subgroup of a group G.
Let ∩i∈I Hi=H
Now we prove H is subgroup
Let a,b∈H
a,b∈Hi for each i∈ I
Since each Hi is a subgroup of G
ab-1 ∈Hi for each i∈ I
ab-1 ∈∩i∈I Hi
ab-1 ∈H
so H is a subgroup
Thus
∩i∈I Hi is a subgroup
Statement: let G be a group and H a subgroup of G. Then the set aHa-1 ={aha-1 ,h∈H } is a subgroup of G.
Proof:
Let x,y∈ aHa-1
x=ah1a-1 ,y=ah2a-1
h1,h2∈H
Now
x,y-1=( ah1a-1 )( ah2a-1)-1
x,y-1= ah1a-1 .(a-1)-1 h2-1 a-1
x,y-1 = ah1a-1ah2-1 a-1
x,y-1=ah1eh2-1 a-1 aa-1=e
x,y-1= ah1h2-1 a-1
H is a subgroup
and h1,h2∈H –>h1h2-1∈H
so
ah1h2-1 a-1 = x,y-1 ∈H
aHa-1 is a subgroup of G.
Statement: the union HUK be two subgroups H and K of a group G is a subgroup of G if and only if either
H is a subset of K or k is a subset of H
Proof:
Let G be a group.
Let H and K be a subgroup of G
Suppose H is a subset of K or k is a subset of H
HUK=K or HUK=H
Since H and k are subgroups
HUK is a subgroup of G
Conversely,
Suppose HUK is a subgroup of G
To prove H is a subset of K or k is a subset of H
We suppose
H is not a subset of k
a∈H but a not belong to K
We also suppose
K is not a subset of H
b∈K but b does not belong to H
Since, a∈H, b∈K
a,b∈ HUK
ab∈ HUK
HUK is a subgroup
ab∈H or ab∈K
When ab∈H
a∈H,a-1∈H H is a subgroup
b=a-1(ab) ∈H H is a subgroup
a-1 a(b) ∈H
eb∈H ,b∈H
when ab∈K
b∈K,b-1∈K K is a subgroup
a=(ab)b-1∈K
a=a(bb-1) ∈K
a=ae∈K
a ∈K
Hence
b∈H or a ∈K
Which is contradiction
Hence
H is not a subset of K.
K is not a subset of H is wrong
Thus
H is a subset of K
K is a subset of H
Summary of a theorem of subgroup
- Two subgroups H and K of a group G, their union HUK need not be a subgroup of G
- The identity of the subgroup is the same as that of the group.
- The inverse of any element of a subgroup is the same as the inverse of that element in the group.
Frequently Asked Question-FAQs
what is a subgroup?
In group theory, a subset H of a group G under a binary operation ∗ is called a subgroup of G if H also forms a group.

 written by
written by 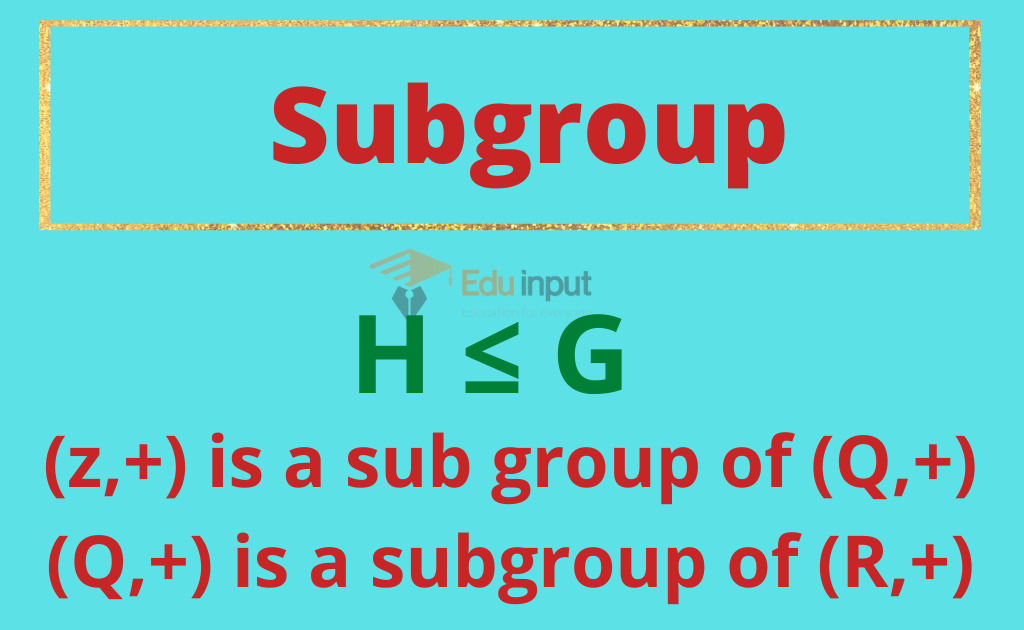



Leave a Reply