Trigonometry Formulas | Sign of Trigonometric Functions in Different Quadrants

The branch of mathematics that focuses on relationships between the sides and angles of triangles is called trigonometry. The word trigonometry comes from the Latin derivative of Greek words for the triangle (trigonon) and measure (metron).

As we know without a formula no operation can be performed. Here are important formulas that help the student to solve difficult problems.

To simplify your calculations, try our Trigonometric Ratios Calculator for quick and accurate results.

Reciprocal Identities

If you need help solving trigonometric functions, check out our Trig Function Calculator for accurate computations.

Even and odd Formulas

sin(−θ) = −sin θ

cos(−θ) = cos θ

tan(−θ) = −tan θ

cosec(−θ) = −cosecθ

sec(−θ) = sec θ

cot(−θ) = −cot θ

Pythagorean Identities

Sin² θ = 1- Cos² θ

Sin² θ + Cos² θ = 1

Sec² θ = 1 + Tan² θ

Cosec² θ = 1+ Cot² θ

sin(π/2-A) = cos A

cos(π/2-A) = sin A

sin(π-A) = sin A

cos(π-A) = -cos A

sin(π+A)=-sin A

cos(π+A)=-cos A

sin(2π-A) = -sin A

cos(2π-A) = cos A

Sum and difference identities

cos (A + B) = cos A cos B – sin A sin B

cos (A – B) = cos A cos B + sin A sin B

sin (A+B) = sin A cos B + cos A sin B

sin (A -B) = sin A cos B – cos A sin B

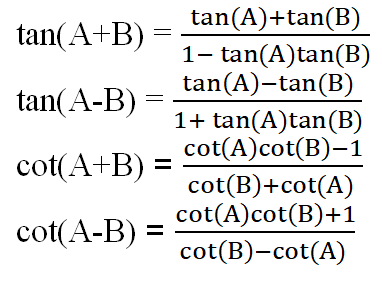
Sign of Trigonometric Functions in Different Quadrants

Quadrant	I	II	III	IV
Sin θ	+	+	–	–
coos θ	+	–	–	+
tan θ	+	–	+	–
sec θ	+	+	–	–
cosec θ	+	–	–	+
cot θ	+	–	+	–