Units of Measures of Angles in Math

Angles are an essential aspect of mathematics and geometry. They are used to measure the amount of rotation or turn between two lines or planes that intersect at a point.

The unit of measure of an angle determines the size of the angle, and there are three main units of measure: degrees, radians, and gradians. In this article, we will discuss each of these units of measure and how they are used in mathematics.

---

---

Key point

• Understanding the unit of measure of an angle is crucial in mathematics and other fields.
• Degrees, radians, and gradians are the most commonly used units of measure of an angle.
• Converting between these units can be done using simple formulas.
• Trigonometric functions rely on the unit of measure of an angle.
• Practical applications of units of measure of an angle can be found in various fields.

---

Introduction

Angles are used to measuring the amount of rotation between two lines or planes that intersect at a point. The unit of measure of an angle determines the size of the angle. There are three primary units of measure of an angle: degrees, radians, and gradians.

 Degrees as a Unit of Measure

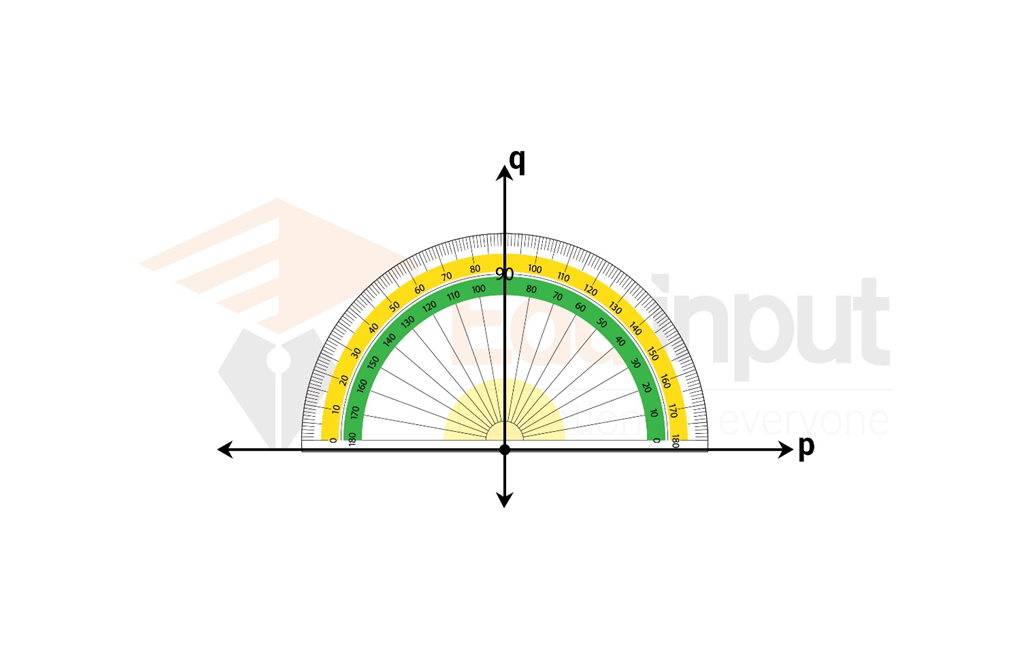
The degree is the most common unit of measure of an angle. One complete revolution of a circle is divided into 360 degrees, where each degree represents 1/360th of a circle. Degrees are denoted by the symbol °.

 Radians as a Unit of Measure

Radians are another unit of measure of an angle commonly used in mathematics. One radian is the angle subtended by an arc of a circle equal in length to the radius of the circle. Thus, one complete revolution of a circle is equal to 2π radians. Radians are denoted by the symbol rad.

 Gradians as a Unit of Measure

Gradians, also known as gons or grads, is another unit of measure of an angle. One complete revolution of a circle is divided into 400 gradians, where each gradian represents 1/400th of a circle. Gradians are denoted by the symbol gon.

Converting between Units of Measure

Converting between units of measure of an angle can be done using conversion formulas. The following are the conversion formulas for degrees, radians, and gradians:

Degrees to Radians: radians = (π/180) × degrees

Radians to Degrees: degrees = (180/π) × radians

Degrees to Gradians: gradians = (400/360) × degrees

Gradians to Degrees: degrees = (360/400) × gradians

Radians to Gradians: gradians = (200/π) × radians

Gradians to Radians: radians = (π/200) × gradians

Trigonometric Functions and Units of Measure

Trigonometric functions such as sine, cosine, and tangent are used to calculate the angles and sides of triangles. The values of these functions depend on the unit of measure of the angle. For example, when using degrees, the trigonometric functions are denoted as sin(θ), cos(θ), and tan(θ). When using radians, the trigonometric functions are denoted as sin(θ), cos(θ), and tan(θ).

 Practical Applications of Units of Measure of Angle

Units of measure of an angle are used in various fields such as engineering, architecture, and surveying. For example, in architecture, angles are used to measure the slope of roofs, stairs, and railings. In surveying, angles are used to determine the direction and location of objects.