What is an Orthogonal Matrix?-Example of Orthogonal Matrix

A square matrix ‘A’ over R is called an orthogonal matrix

If AA^t=I

OR

A^t=A^-1

A = a square matrix

A^t=transpose of A

I=identity matrix of the same order as ‘A’

A^-1=inverse of A

The product of the square matrix and it is transposed gives an identity matrix same order is called an orthogonal matrix. Or we can say A square matrix with real numbers is called an orthogonal matrix if its transpose is equal to its inverse of a matrix.

For example:-

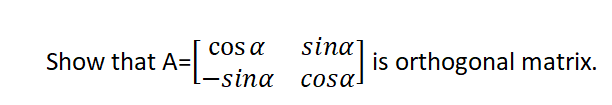
Solution:

Given matrix

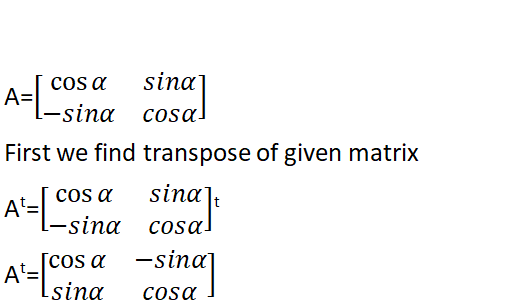
According to the definition of an orthogonal matrix

Prove that

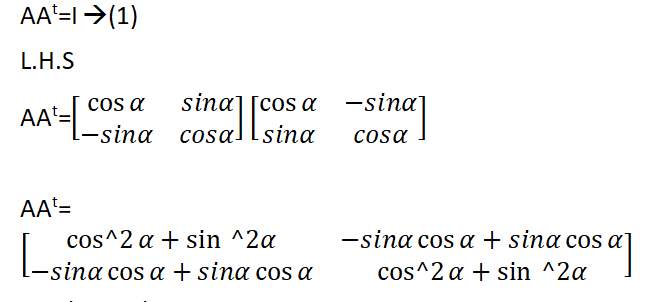
 We know that

Cos² α+ sin²α=1

-sinα cosα+sinα cosα=0

Summary

• Every identity matrix is an orthogonal matrix
• If A is an orthogonal matrix then A^-1 is also an orthogonal matrix
• If A is an orthogonal matrix then A^t is orthogonal
• If A is an orthogonal matrix then Aⁿ is orthogonal
• The product of two orthogonal matrices is also orthogonal