What is Divisor Mean in Math?-Definition, And Formula

A divisor divides a number into equal parts or is a number that divides another number. A divisor without, we cannot divide numbers. In division, there are four important terms that are used – dividend, quotient, divisor, and remainder.

The division is a way of distributing things equally in groups. The number that needs to be divided is known as the ‘dividend’ and the total number of equal groups in which it has to be divided is said to be the ‘divisor’. The number that is left out without forming a group is termed is said to be the ‘remainder’.

What is Divisor?

A divisor divides a number into equal parts. The number that is being divided is said to be the dividend and the number that divides it is said to be the divisor.

Divisor Meaning

A number that divides another number by leaving a zero remainder is called a divisor.

There are various ways to write a division problem. The following figure shows the distinct ways in which division is expressed and it shows how to identify the divisor, the dividend, and the quotient.

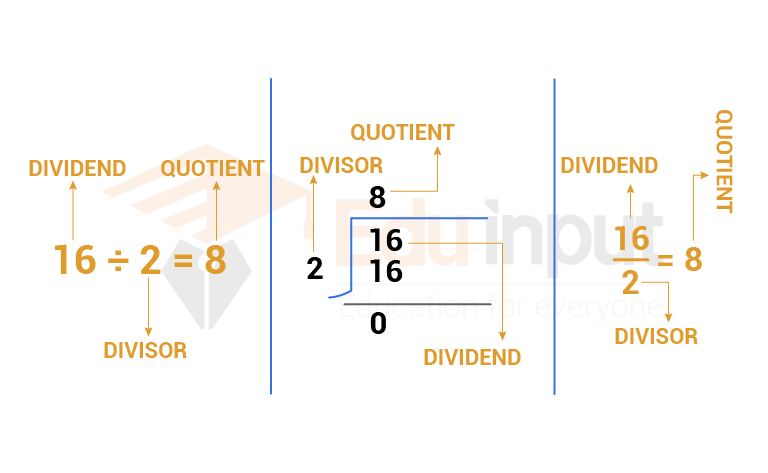
How to find the Divisor

Without divisors, division is not possible. It means identifying a divisor is quite very simple.

 For example, if we need to divide the number 40 by 5, it can be denoted as 40 ÷ 5= 8. Here, the number 40 is the dividend, the number 5 is the divisor, and the number 8 is the quotient.

Sometimes we know the value of the dividend and the quotient and we need to calculate the divisor. In this case, we apply the divisor formula.  Learn about the divisor formula in the following section.

Divisor formula:

The divisor formula is made for two situations – with or without a remainder:

• If the remainder is equal to zero (0), then Divisor = Dividend ÷ Quotient.
• If the remainder is not equal to0, then Divisor = (Dividend – Remainder) ÷ Quotient.

For example:

Determine the divisor if the dividend is 54 and the quotient is 6.

Solution:

We know that quotient = 6, dividend = 54,. So, apply the divisor formula,

 Divisor = Dividend ÷ Quotient. Values in the formula, we get, Divisor = 54 ÷ 6 = 9.

Given that the divisor = 9.

For example:

Calculate the divisor if the dividend is 42, the quotient is 5 and the remainder is 2.

Solution:

We know that dividend = 42, remainder = 2, quotient = 5.  So,  apply the divisor formula, Divisor = (Dividend – Remainder) ÷ Quotient. The values in the formula, we get, Divisor = (42 – 2) ÷ 5 = 40 ÷ 5 = 8. Therefore, the divisor = 8.

Divisor Facts

Here is a list of facts related to the divisor.

• When the dividend is the same as the quotient then the divisor is 1.

For example, 54 ÷ 1 = 54

• When the divisor and the dividend are equal in a division problem, the quotient is 1.

 For example, 25 ÷ 25 = 1

• A quotient is a number that is obtained upon dividing a dividend by a divisor, and any number that is left over after the division is said to be the remainder.
• The remainder is always less than the divisor.
•   The divisor has completely divided the dividend. It means the remainder is zero
• When the divisor is greater than the dividend, then the answer number will be a decimal number. For example, 55 ÷ 100 = 0.55

Difference between Divisor and factor

We know that divisor is a number that divides the dividend. When a divisor divides the dividend completely and leaves zero remainders, that divisor is said to be a factor of that number. Thus, all divisors need not be factors of a number always but all factors of a number are divisors.

For example:

Factors of 6 = 1, 2, 3, and 6. it means 6 is completely divisible by 1, 2, 3, 6. Therefore, all these factors are divisors in this case.

For example:

Divide 13 by 5. If we divide 13 by 5 we get the remainder is 3and 2 as the quotient. This means 12 ÷ 5 = 3, Remainder = 3. In this case, the divisor is 5, but 13 is not completely divisible by 5. So, 5 is not a factor of 13 but it is a divisor of 12 as it gives a remainder of 3.

Hence, all divisors are not factors but

 all factors are divisors

 Summary:

• A divisor cannot be zero because when a number is divided by zero the answer is undefined.
• When zero is divided by any divisor it always answers zero as the quotient.