Polynomial Function | Remainder Theorem, Factor Theorem, and Synthetic Division

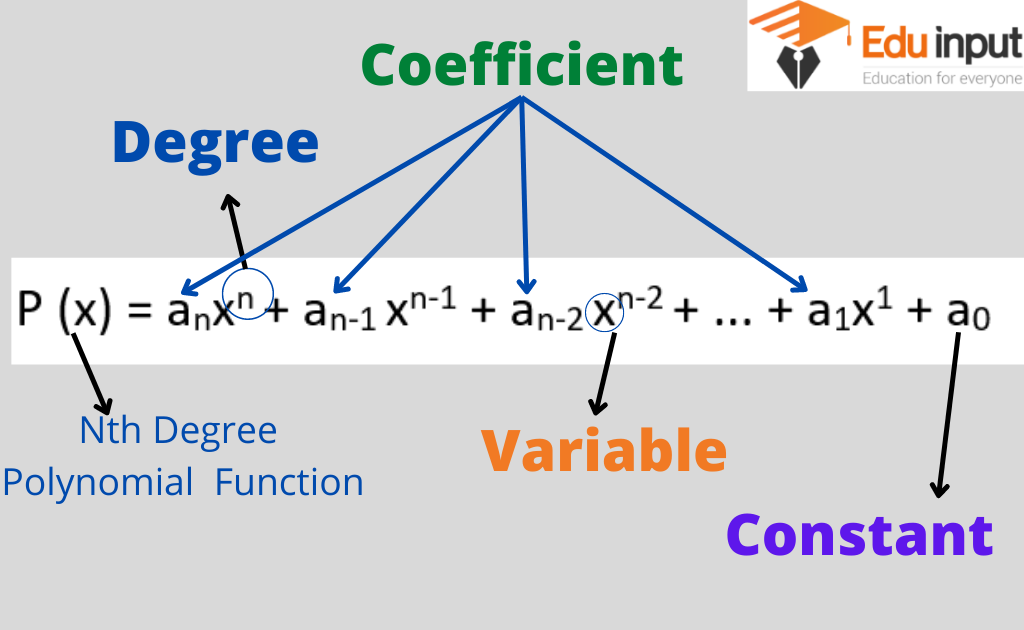
A polynomial function in x is an expression of the form

a_nx ⁿ+a_n-1 x^n-1+….+a_1nx+a₀,     a≠0 –> (i)

Where n is a non-negative integer and the coefficients a_n,a_n-1,…,a₁ and a₀ are real numbers.

It can be considered as a polynomial function of the highest power of x in a polynomial in x is called the degree of the polynomial. So the expression (i), is a polynomial of degree n.

For example:

The polynomials x²-3x+2, 3x³+2x²-5x+4 are degree 2 and 3 respectively.

Dividend =(divisor)(quotient)+remainder

Remainder Theorem:

If a polynomial f(x) of degree n≥1, n is a non-negative integer divided by (x-a) til no x-term exists in the remainder, then f(a) is the remainder.

Proof: suppose we divide a polynomial f(x) by x-a.Then there exists a unique quotient q(x) and a unique remainder R such that f(x)=(x-a)q(x)+R–>(i)

Substituting x=a in equation (i), we get

f(a)= (a-a)q(a)+R

f(a) =0+R

f(a)=R

Hence reminder =f(a)

A reminder obtained when f(x) is divided by (x-a) is the same as the value of the polynomial f(x) at x=0

For example: Find the remainder when the polynomial x³+4x²-2x+5 is divided by x-1.

Solution: let f(x)= x³+4x²-2x+5 and

x-a=x-1

we have

a=1

Remainder =f(1)                   (by remainder theorem )

Remainder =(1)³+4(1)²-2(1)+5

Remainder =1+4-2+5

Remainder =8

For example: find the numerical value of K if the polynomial x³+kx²-7x+6 has a remainder of -4 when divided by x+2.

Solution: let f(x)= x³+kx²-7x+6  and x-a=x+2, we have a=-2

Remainder =f(-2)                 (by remainder theorem )

Remainder =(-2)³+k(-2)²-7(-2)+6

Remainder = -8+4k+14+6

Remainder =4k+12

Given that remainder =-4

4k+12=-4

4k=-4-12

4k=-16

K=-16/4

K=-4

Factor Theorem:

The polynomial( x-a) is a factor of the polynomial f(x) if and only if f(a)=0 i.e (x-a) is a factor of f(x) if and only if x=a is a root of the polynomial equation f(x)=0.

Proof: suppose g(x) is the quotient and R is the remainder when a polynomial f(x) is divided by(x-a) then by the remainder theorem

f(x)=(x-a)g(x)+R

Since f(a)=0

R=0

f(x)=(x-a)g(x)+0

f(x)= (x-a)g(x)

(x-a) is a factor of f(x).

Conversely, if (x-a) is a factor of f(x), then

R=f(a)=0

Hence proved

 To determine if a given linear polynomial (x-a) is a factor of f(x), all we need to check is whether f(a)=0

For example: show that (x-2) is a factor of x⁴-13x²+36

Solution: let f(x)= x⁴-13x²+36 and x-a=x-2 we have x=2

Remainder =f(2)                     (by remainder theorem )

Remainder=(2)4-13(2)2+36

Remainder =16-52+36

Remainder =52-52

Remainder =0

(x-2) is a factor of x⁴-13x²+36

Synthetic Division:

There is a shortcut method for the long division of a polynomial f(x) by a polynomial of the form(x-a). This process of division is called synthetic division.

Outline of the Method:

• Write down the coefficients of the dividend f(x) from left to right in decreasing order of powers of x .insert 0 for any missing terms.
• To the left of the first line, write an of the divisor (x-a).
• Use the following patterns to write the second and third lines :

Vertical pattern (↓)

Diagonal pattern (↗)

Add term

Multiply by a

For example:

Use synthetic division to find the quotient and the remainder when the polynomial x⁴-10x²-2x+4 is divided by x+3.

Solution: let f(x)= x⁴-10x²-2x+4

 f(x)= x⁴ +0x³-10x²-2x+4

And x-a=x-(-3)

x=-3

Dividend x⁴-10x²-2x+4

  Quotient =x³-3×2-x+1 Remainder =1

Frequently Asked Question -FAQs