Three Cube Roots Of Unity

The cube roots of unity are the cube roots of one.

Example:

Proof:    

Let x be the cube roots of unity

X³=1

X³-1=0

X³-1³=0                       

1³=1

By using

a³ – b³= (a-b) (a²+ab+b²)

X³ -1³=(x-1) (x²+x+1²)

(x – 1) (x² + x+1²)=0

X – 1=0                 x²+x+1=0

X=1                            x²+x+1=0

                           By using quadratic formula

Thus the three cube roots of unity are:

We know that I am called a complex number.

    Properties of cube roots of unity

• Each complex cube root of unity is square of the other
• The Sum of cube roots of unity is zero
• Product of cube roots of unity is one
• Each complex cube root of unity is reciprocal to other
• Each complex cube root of unity is conjugate of each   other
• Each complex cube root of unity is the multiplicative inverses of each other
• For an is equivalent to  one  of the cube roots of unity

Each complex cube root of unity are square of the other

Complex cube roots of unit

Product of cube roots of unity is one

Proof:

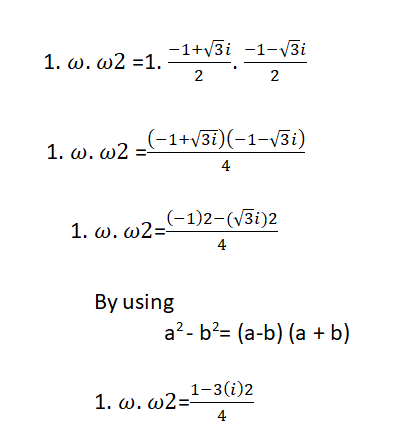
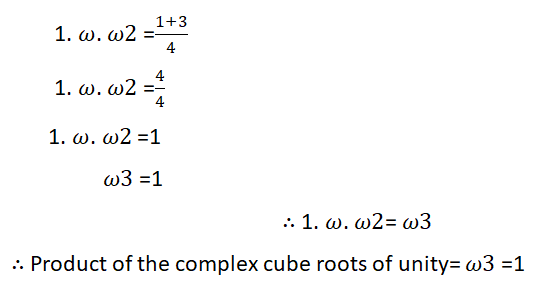
Each complex cube root of unity is reciprocal of each other

Proof:

As we know

Each complex cube root of unity is reciprocal to each other.

Each complex cube root of unity is conjugate of each other

Proof:

Let

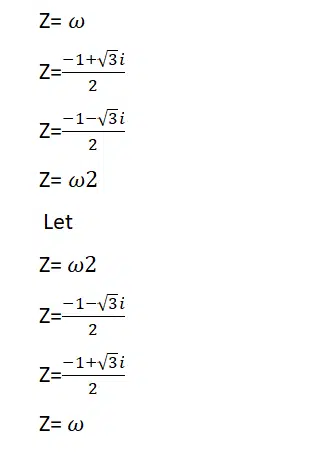
Hence proved

Each complex cube root of unity is conjugate of each other

For any

equivalent to one of the cube roots of unity.

Frequently Asked Question-FAQs