Coordinates of A Point in Three Dimensions

Defining the location of points in space requires a coordinate system. Just as a two-dimensional coordinate system uses an x-axis and y-axis, a three-dimensional system adds a z-axis to describe points in three dimensions.

In this article, we will discuss the coordinates of a point in three dimensions in mathematics.

Three Dimensional Coordinate System

The x, y and z number lines form three perpendicular axes that intersect at a central origin point. The x-axis runs left-to-right, the y-axis forward-backward, and the z-axis up and down.

Imagine you have a point P in three-dimensional space. Now, if you drop perpendiculars from P to the three axes (let’s call them BC, BA, and PB), the lengths of these perpendiculars are like the addresses of P. We call these lengths x, y, and z.

When we talk about the coordinates of a point, we always list them in a specific order. The x-coordinate comes first, followed by the y-coordinate, and then the z-coordinate.

So, for every point in space, you can describe it using three real numbers, forming what we call an “ordered 3-tuple.”

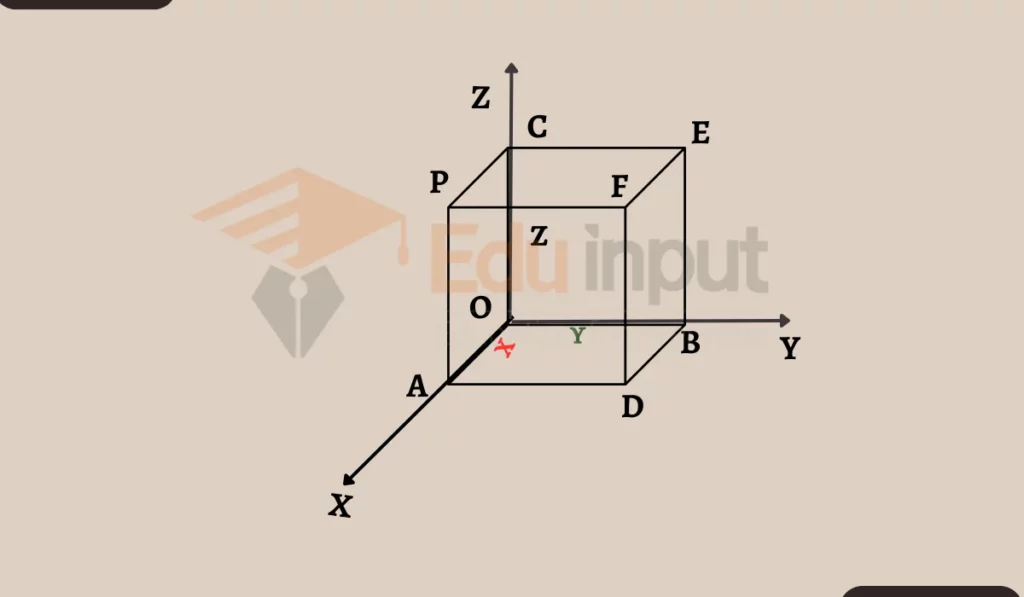
The coordinates of P in the preceding figure are denoted by (x, y, z). The origin O’s coordinates are (0, 0, 0). Additionally, since point A is entirely on the x-axis, its coordinates are given by (x, 0, 0). In a similar manner, any point’s coordinates on the y-axis are expressed as (0, y, 0), while its coordinates on the z-axis are expressed as (0, 0, z). Additionally, any point in the three planes—XY, YZ, and ZX—will have coordinates of (x,y,0), (0,y,z), and (x,0,z), respectively.

Remembering Coordinate Positions

An easy way to remember coordinate positions is by using your hands:

• Hold your right hand out with fingers straight up – Your thumb points in the +x direction to the right, index finger in the +y direction forward, and middle finger in the +z direction up.
• Bending a finger back toward your wrist indicates the negative direction along that axis.
• Your palm centered where the axes meet represents the origin (0, 0, 0).

Applications

Defining points with coordinates is essential for applications like:

• Describing 3D objects in fields like engineering and computer graphics – The vertices of 3D shapes can be precisely positioned using coordinate triplets
• Identifying locations in 3D space for navigation systems, games, virtual reality, etc.
• Creating three-dimensional graphs to visualize data and functions
• Performing calculations and proofs in 3D geometries in mathematics

Without the coordinate system for identifying point locations, applications dealing with 3D structures, data, and spaces would not be possible.

FAQs

I hope this helps explain the basics of the three-dimensional coordinate system! Let me know if you need any clarification or have additional questions.