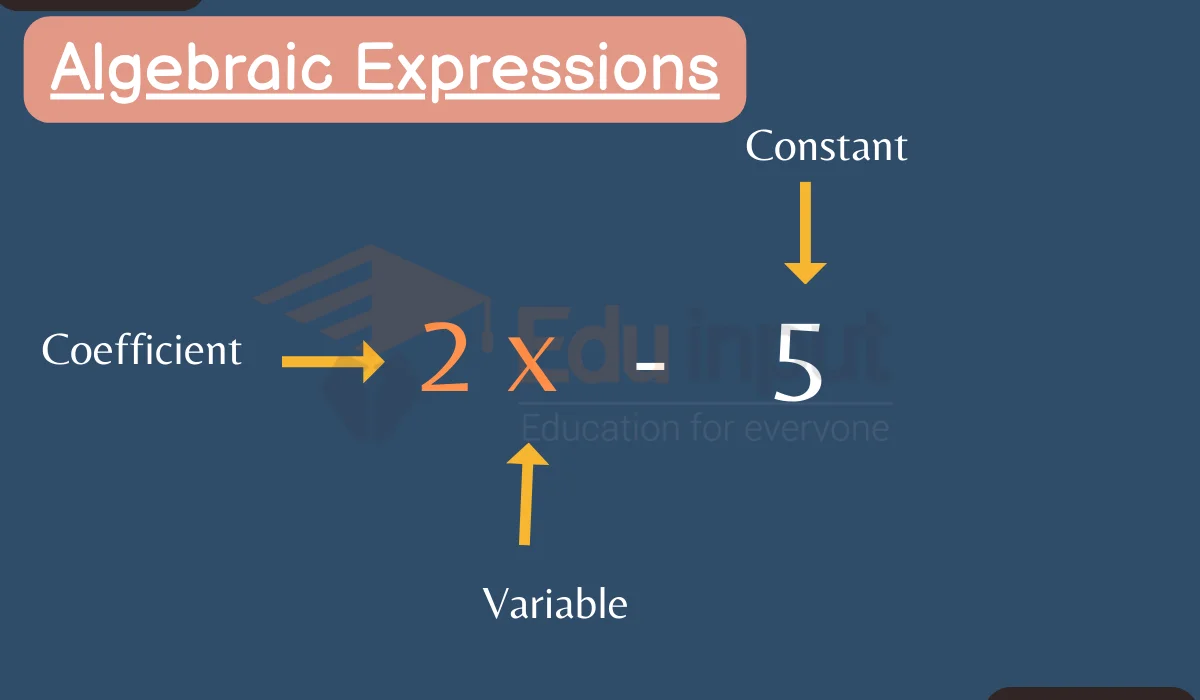
Distributive Property in Algebra
Distributive property is one of the most important rules in algebra. It allows you to simplify algebraic expressions by distributing multiplication over addition and subtraction.
Distributive property states that multiplying a sum by a number gives the same result as multiplying each addend separately and then adding the products.
In this article, we will discuss distributive property in algebra.
Distributive Property with Multiplication
Distributive property can be expressed in the following way for multiplication:
a(b + c) = ab + ac
This means that multiplying a sum in parentheses by a value outside the parentheses is the same as multiplying each part of the sum individually and then adding the results.
Example
3(x + 5) = 3x + 15
To show this:
3(x + 5)
= 3x + 3(5)
= 3x + 15
So the distributive property allowed us to distribute the 3 to each part of the sum x + 5.
Distributive Property with Division
Distributive property works similarly with division:
a/(b + c) = a/b + a/c
Example
6/(2 + 3)
= 6/2 + 6/3
= 3 + 2
= 5
So the distributive property allowed us to divide 6 separately by the 2 and 3 in the denominator.
Examples Using the Distributive Property
Example
4(x – 2)
4(x – 2) = 4x – 8
Example
(x + 4)/5
(x + 4)/5 = x/5 + 4/5
Example
5(x – 3y)
5(x – 3y) = 5x – 15y
FAQs
What is the formula for the distributive property?
The distributive property formula is: a(b + c) = ab + ac. This shows that multiplying a sum in parentheses by a value outside the parentheses is the same as multiplying each part separately and then adding the products.
How do you use the distributive property to simplify expressions?
To use the distributive property, you break up the terms in parentheses and multiply or divide each term separately, then combine the results. This allows you to simplify the expression step-by-step.
What is an example that uses the distributive property?
Here is an example: 4(x + 2) = 4x + 8. Using the distributive property, we broke up the term in parentheses, multiplied each term by 4, then combined the results.
Can the distributive property be used with subtraction?
Yes, the distributive property works with subtraction in the same way. For example: a(b – c) = ab – ac. The subtraction sign is distributed to each term within the parentheses.



Leave a Reply