Algebraic Expressions

Algebraic expressions are like using letters instead of specific numbers. Think of them as a secret code where we use letters like x, y, or z to stand in for numbers we don’t know yet. These letters are called variables. Sometimes, we mix these letters with actual numbers, which are called constants. When we put a number in front of a letter and multiply them, that number is called a coefficient.

So, algebra is all about using these letters and numbers to solve puzzles and figure things out.

In this article, we will discuss algebraic expressions and how to solve them.

What Are Algebraic Expressions?

Algebraic expressions are mathematical phrases that consist of variables, constants, and operations.

They are used to represent real-life situations, equations, and relationships between different quantities. For example,

• 2x + 1
• 3x² + 5y – 7
• 9x

Components of Algebraic Expressions

These are components of algebraic expressions.

• Variables
• Constants
• Operations

Variables and Constants

Variables are symbols (usually letters) that represent unknown values.

Constants, on the other hand, are specific, unchanging values. Learning to differentiate between them is fundamental.

Operations

In algebraic expressions, operations include addition, subtraction, multiplication, and division.

Example

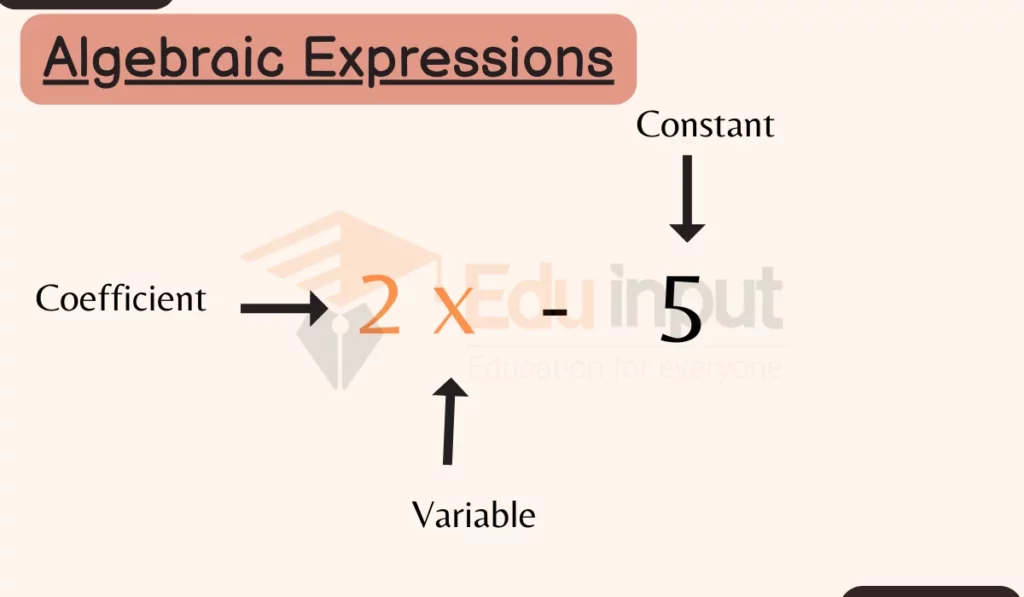
In the above expression (i.e. 2x – 5),

• x is a variable, whose value is unknown to us which can take any value.
• 2 is known as the coefficient of x, as it is a constant value used with the variable term and is well defined.
• 5 is the constant value term that has a definite value.

Simplifying Algebraic Expressions

To simplify algebraic expressions, we group similar terms together and combine them.

Take the expression:
2x^2 – 3x + 4x^2 – x + 5

Combine like terms:
(2x^2 + 4x^2) + (-3x – x) + 5

Simplified form:
6x^2 – 4x + 5

Adding Algebraic Expressions

When adding algebraic expressions, we combine like terms and perform the addition.

Example

(3x^2 + 2x – 5) + (5x^2 – 3x + 7)

= (3x^2 + 5x^2) + (2x – 3x) + (-5 + 7)

=8x^2 – x + 2

Subtracting Algebraic Expressions

Subtraction is like addition but with the additive inverse of the second expression.

Example

(4x^2 – 2x + 3) – (2x^2 + 2x – 1)

= (4x^2 – 2x^2) + (-2x – 2x) + (3 – (-1))

= 2x^2 – 4x + 4

Multiplying Algebraic Expressions

To multiply expressions, we distribute each term in the first expression to each term in the second and then combine like terms.

Example

(2x + 3)(x – 1)

= 2x * x + 2x * (-1) + 3 * x + 3 * (-1)

= 2x^2 – 2x + 3x – 3

= 2x^2 + x – 3

Dividing Algebraic Expressions

Division involves factoring and canceling out common terms.

Example

(6x^2 + 3x) / (3x)

= 3x(2x + 1) / 3x

= 2x + 1

Types of Algebraic expression

There are 3 main types of algebraic expressions which include:

• Monomial Expression
• Binomial Expression
• Polynomial Expression

Monomial Expression

A monomial is like a special agent in the world of algebra because it has only one job or term. It’s as simple as it gets.

For example, 3x or 8y.

Binomial Expression

Binomial express is an algebraic expression with two terms that are different from each other.

For example, 5xy + 8 or xyz + x³.

Polynomial Expression

A polynomial is an expression with more than one term, and all of these terms have powers (exponents) that are non-negative whole numbers.

For example, ax + by + ca or x³ + 2x + 3.

Algebraic Expression Formulas

Formula	Expression
(a + b)²	a² + 2ab + b²
(a – b)²	a² – 2ab + b²
(a + b)(a – b)	a² – b²
(x + a)(x + b)	x² + x(a + b) + ab
(a + b)³	a³ + 3a²b + 3ab² + b³
(a – b)³	a³ – 3a²b + 3ab² – b³
a³ + b³	(a + b)(a² – ab + b²)

These formulas are essential tools in algebra, making it easier to solve equations and work with algebraic expressions.

Algebraic expressions are the gateway to understanding algebra. They are versatile tools used in everyday life, from calculating finances to solving complex mathematical problems.

FAQs