Division of Algebraic Expressions

In algebra, division is one of the fundamental operations that we use to solve equations and understand the relationships between variables.

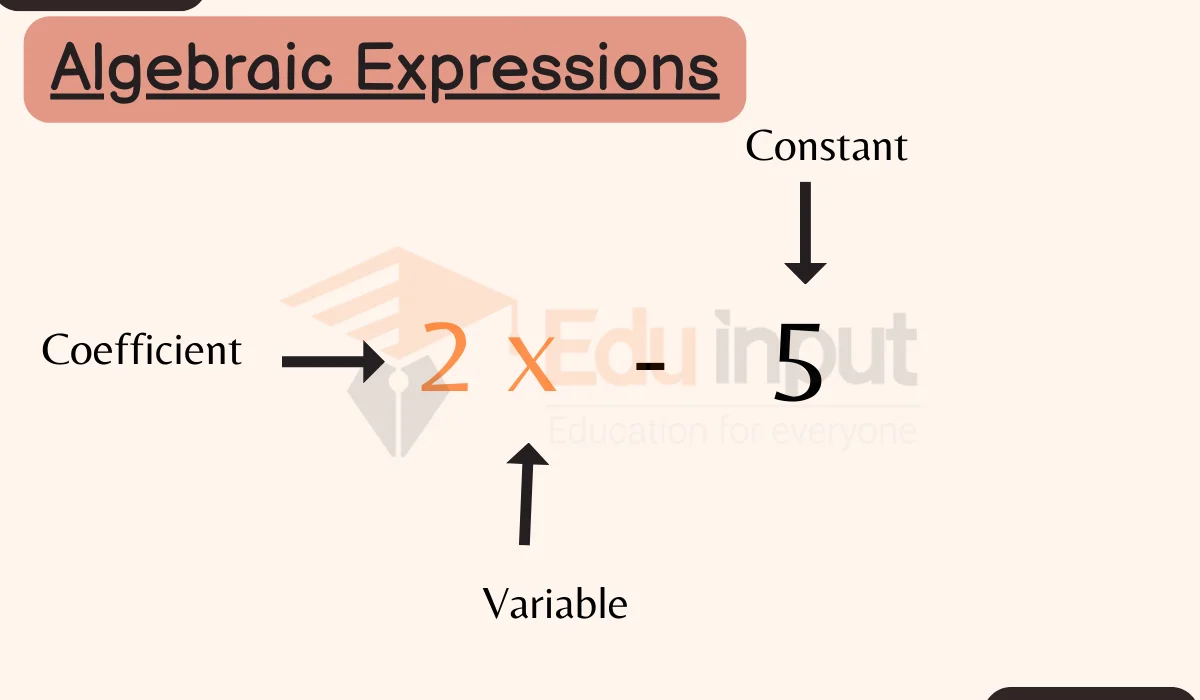
Algebraic expressions are mathematical statements that include variables (like ‘x’ or ‘y’), constants (numbers), and operators (addition, subtraction, multiplication, division).

In this article, we will discuss the division of algebraic expressions in simple terms.

Division by a Constant

When you divide an algebraic expression by a constant, you can make it easier by dividing each term by that constant.

Example

Divide (8x^2 – 16x) by 4.

First, divide each term by 4:

(8x^2 / 4) – (16x / 4) = 2x^2 – 4x

Division by a Monomial

When dividing by a monomial, you divide each term of the expression by that monomial.

Example

Divide (6y^2 – 18y) by 3y.

Start by multiplying by the 3y,

(6y^2 – 18y) / (3y) = (6y^2/ 3y – 18y/ 3y)

= 2y – 6

Division by a Polynomial

Dividing by a polynomial follows similar principles as division by a monomial.

Example

Divide (12x^3 – 6x^2 + 9x) by (3x^2).

Multiply each term by 3x^2,

(12x^3 – 6x^2 + 9x) / (3x^2) = (12x^3/ 3x^2 – 6x^2/ 3x^2 + 9x/ 3x^2)

= 4x – 2 + 3/x

Solved Examples Division of Algebraic Expressions

Example

Divide the algebraic expression (4x^2 – 12xy) by 4.

Solution:

To divide by a constant, you simply divide each term of the expression by that constant.

(4x^2 – 12xy) ÷ 4

= (4x^2 ÷ 4) – (12xy ÷ 4)

= x^2 – (12xy ÷ 4)

= x^2 -3xy

So, the result is: x^2 – 3xy.

Example

Divide the algebraic expression (9x^3y^2 – 18x^2y) by 3x.

Solution

When dividing by a monomial, you divide each term of the expression by that monomial.

(9x^3y^2 – 18x^2y) ÷ 3x = (9x^3y^2 ÷ 3x) – (18x^2y ÷ 3x)

= 3x^2y^2- (18x^2y ÷ 3x)

= 3x^2y^2-6xy

So, the result is: 3x^2y^2 – 6xy.