Elastic Collision-One Dimensional And Two Dimensional Elastic Collision
An elastic collision is an encounter between two bodies in which the total energy of the two colliding bodies is the same. In a perfectly elastic collision, there is no net conversion of kinetic energy into other forms(potential energy).
What is Elastic Collision?
An elastic collision is a collision in which there is no net loss of energy in the system. In an elastic collision, both momentum and kinetic energy are constant.
The potential energy associated with a repulsive or attractive force between the particles is converted to kinetic energy during the collision of small objects. If the angle between the force and the relative velocity is not straight, then the potential energy is converted back to the original energy when the particles move with this force. The angle between the force and the relative velocities is very close.
In an inelastic collision, momentum is conserved but kinetic energy is not. This means that the total momentum of the objects before and after the collision is the same. However, kinetic energy is lost due to the action of internal friction. In a traffic collision, some of the kinetic energy of the car or cars is converted to some other form, such as heat or sound. A perfectly inelastic collision occurs when the objects stick together.
Elastic collision in one dimension
in two bodies collision in which the notion of the colliding objects occur along a straight line before and after the collision. In elastic collision kinetic energy and momentum of the system remain constant
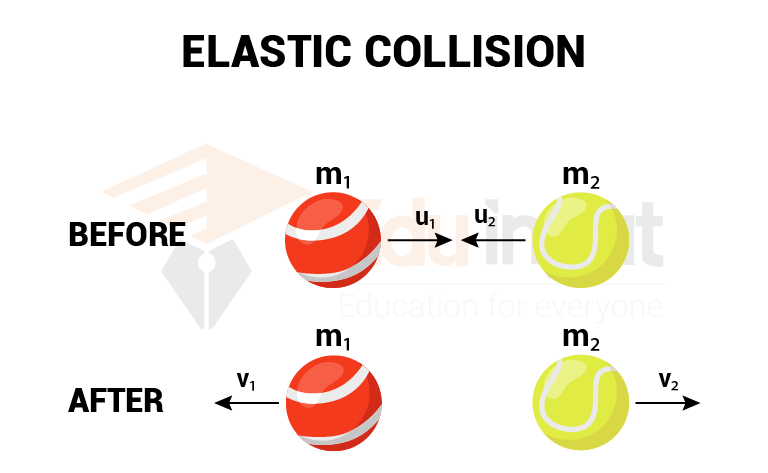
According to the law of conservation of momentum
m1u1 + m2u2 = m1v1 + m2v2
According to the law of conservation of kinetic energy
(1/2) m1u12 + (1/2) m2u22 = (1/2) m1v12 + (1/2) m2v22
Two-dimensional Elastic collision
In the case of two colliding bodies in two dimensions, the motion of the bodies is determined by the three laws of momentum, energy, and inertia. Each body’s overall velocity must be split into two different velocities, one at the point of contact and the other along the line of collision.
The velocities that are related to the point of the collision do not change since the collision only causes force along the line of collision. In the same way as a one-dimensional collision, the velocities along the line of collision can be used in the same equations.
The final velocities can be calculated from the two new component velocities and will be dependent on the point of collision. Many bodies in the framework of a two-dimensional gas are studied for two-dimensional collision studies.
Applications of Elastic Collision
The amount of force an object experiences during a collision is determined by the collision time. The force acting on the object is smaller when the collision time is greater. To maximize the force experienced by an object during a collision, the collision time must be decreased. The time between the collision and the force needs to be increased.
There are a number of real-world applications for these phenomena. The collapse time and the effect of force on objects during a collision can be reduced by the use of Airbags in automobiles. Extending the time required to stop the passenger and the driver is accomplished by the Airbag.






Leave a Reply