Fundamentals of Trigonometry | Angle, Vertex of angle, Radian, Circular system

Fundamentals of trigonometry include angle, vertex of the angle circular system, etc

The word trigonometry is derived from three Greek words: Trei (three), Goni (angles), and Metron (measurement). Exactly it means measurement of a triangle.

Angle:

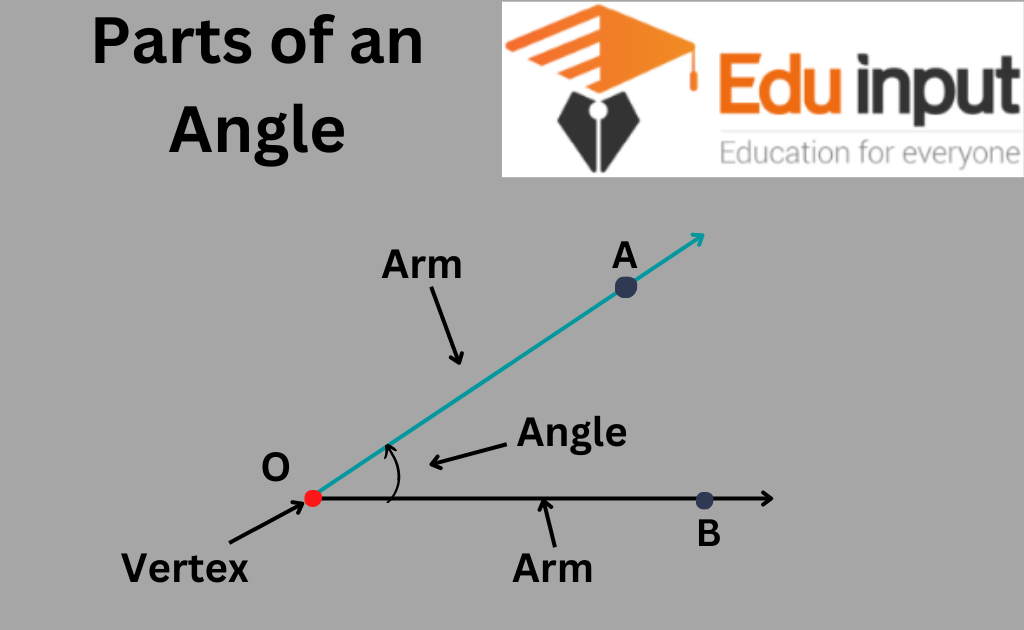
Two rays with a common starting point from an angle. One of the rays of angle is called the initial ray (initial side) and the other is the terminal ray (terminal side).

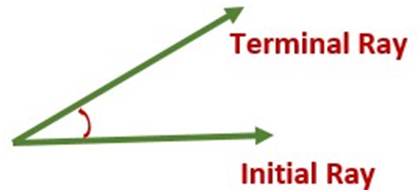
Vertex of Angle:

The point where the arms of an angle meet is called the vertex of the angle.

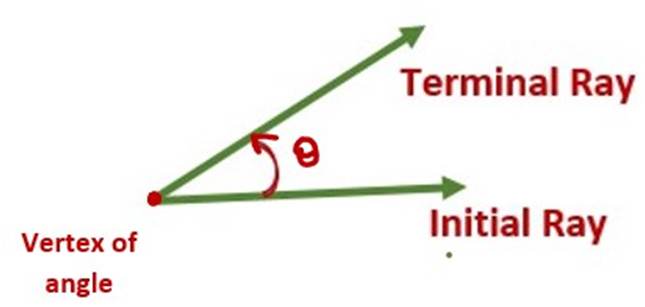
Positive and Negative angles:

An angle is said to be positive if its rotation is anti-clockwise.

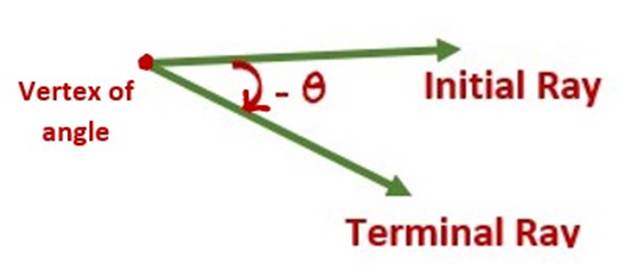
An angle is said to be negative if its rotation is clockwise

Sexagesimal system

A number system with a base of 60. It uses the concept of degrees, minutes, and seconds for measuring angles. It is also called the English system or the Do M’ S’’ system.

Degree, Minute, and Second Measure of an Angle:

If we divide a circle into 360 equal parts, the angle made by one part at the center of the circle is called an angle of one degree denoted by 1o. The 60th part of the degree is called one minute denoted by 1’ and the 60th part of one minute is called one second denoted by 1″.

Conversion to Decimal form:

180^o6’21’’

=180^o + 6’ + 21’’ = [18 + 6(1/60) + 21(1/60 x 60)]^o

= [18 + 1/10 + 7/20 x 60]^o

= [18 + 0.1 + 0.005833]^o

= 18.105833^o

Circular System:

A system in which angles are measured in radians is called a circular system.

Radian:

Radian is the measure of the angle subtended at the center of the circle by an arc, whose length is equal to the radius of the circle.

Prove of l = rθ

Let r be the radius of a circle having a center at point O. Let θ radian be the angle made by an arc of length l at the center of the circle. We know that.

Ratio of arc length l to the circumference 2πr of a circle is same as ratio of θ to 2π. i.e.

l : 2πr = θ : 2π

= l/2πr = θ/ 2π

= 2πl = 2πrθ

l = rθ

Relation between Degree and Radian measure:

Since l = rθ

θ = l/r, since circumference of a circle is of length 2πr

So θ = 2πr/ r

θ = 2π. But for one complete revolation θ = 360^o

2π radians = 360^o

π radians =  180^o

1radian = 180^o/ π = 57.296^o ≈ 57.3^o and 1^o = π/180 radian ≈ 0.0175 radian

Formulae:

10 = 60’

1’ = 60’’

1^o = 60’’

πrad = 180^o

1^o = 0.01745 radians

l = rθ

Area of circular sector =1/2 r²θ

Sin2θ + cos2θ = 1

Sec2θ – tan2θ = 1

 

  

Frequently Asked Question-FAQs