Introduction to operation of set-Edu input

There are four types of set operations.

1. Union of sets.

2. Intersection of set s.

3. Difference of sets.

4. Complement of a set.

1. Union of Sets:

If we have two sets A and B, then the union both sets will contain all the elements of set A and B

Example:

A= {a, b, c, d, e}, B= {a, b, c}

AUB= {a, b, c, d, e} U {a, b, c}

AUB= {a, b, c, d, e}

A= {a, b, c, d, e}, B= {a, b, c}

BUA= {a, b, c} U {a, b, c, d, e}

BUA= {a, b, c, d, e}

The green area shows the AUB and BUA.

2. Intersection of Sets

If we have two sets A and B then the intersection of both sets will be the common elements of A and B sets.

Example:

A= {4, 6, 9, 10, 12}, B= {1, 3, 5, 7, 9, 11, 13}

A∩B= {4, 6, 9, 10, 12} ∩ {1, 3, 5, 7, 11, 13}

A∩B= {9} The intersection of B∩A will also be same as A∩B.

The green area shows the A∩B and B∩A

3: Difference of Sets

If we have two sets A and B, and we want to find the A- B, The difference of sets will contain all elements of set A which does not belong to set B.

Example:

A= {1, 2, 3, 4, 5, 6, 7, 8}, B= {1, 2, 3, 4, 5}

A-B = {1, 2, 3, 4, 5, 6, 7, 8} – {1, 2, 3, 4, 5}

A-B = {6, 7, 8}

B-A = {1, 2, 3, 4, 5} – {1, 2, 3, 4, 5, 6, 7, 8} B-A= { }

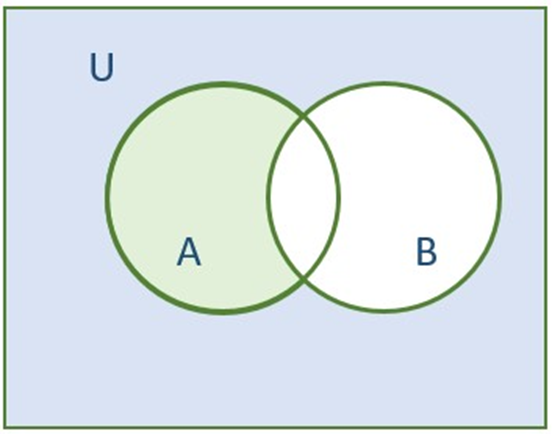
The green area showing the A-B.

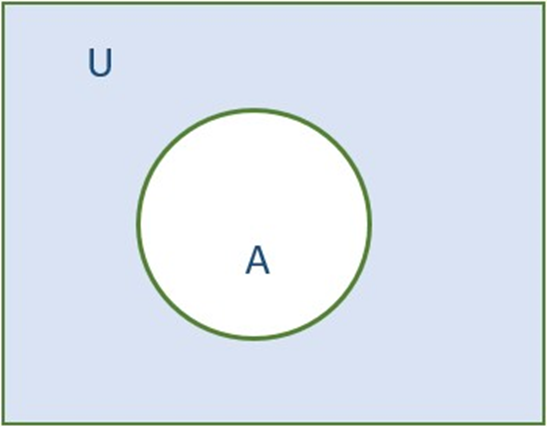
4: Complement of Set

We know, that when U be the universal set and A is a subset of U. Then the complement of A is the set of all elements of U which are not the elements of A.

The complement of set A is denoted by A^’

Example:

U= {a, b, c, d, e, f, g, h,}, A= {a, b, c, d}

A^’ = U-A

U-A= {a, b, c, d, e, f, g, h}-{a, b, c, d} U-A= {e, f, g, h}

Frequently Asked Question-FAQs