What is Set in mathematics? Explained with examples

Definition of set

Set is a collection of well-defined and distinct objects.

Set is denoted by capital letters (A, B, C…). The member of sets are represented by small letters.
Sets are enclosed in curly brackets.

---

Give it a go

Introduction to operation of set

Properties of sets

---

Watch Set related video lecture

Methods to write a set

There are three methods of sets.

1. The Descriptive Method.

2. The Tabular Method.

3. Set builder Method.

The Descriptive Method:

In the descriptive method, the set is represented in words.

For Example:

The set of natural numbers.

The set of alphabets.

The Tabular Method

In the tabular method, sets are represented by elements within braces. For example.

N = {1, 2, 3, 4, …}

A = {apple, banana, mango}

Set builder Method

Set–builder notation is a mathematical notation to describe a set by representing its elements or explaining the properties that its members must satisfy.

For Example:

A= {x|x is first ten natural number}

B= {x|x ∊ N ∧ x ≤ 5}

Types of set

There are different types of sets.

• Empty set
• Singleton set
• Finite set
• Infinite set
• Equal set
• Equivalent set
• Subset
• Universal set

Empty Set

A set having no elements. It is denoted by the symbol ∅ and {}

For Example: A= {}, B=∅

Singleton Set

A set having only one element is called a singleton set.

For Example: A= {1}, B= {2}, C=a {a}

Finite Set

Finite set has limited number of elements.

For example: N = {1, 2, 3, 4, 5}, N= {x|x ∊ N ∧ x ≤ 5}

Infinite Set

An infinite set has an unlimited number of elements. For example:

W= {0, 1, 2, 3, …}

Set of all integers.

Equal Set

Two or more sets are said to be equal sets if they have the same number of elements and same elements then set A is equal to set B and set B is equal to set A.

A= {a, b, c, d}, B= {a, b, c, d} Here, n(A)=n(B) and also have same elements.

Equivalent Set

Two or more sets are said to be equivalent sets if they have the same number of elements but not the same elements then set A is equivalent to set B and set B is equivalent to set A. For example:

A= {1, 2, 3, 4}, B= {a, b, c, d}

In these sets n(A) = n(B), but have not same elements.

Subset

If A and B are two sets, set A is said to be a subset of set B if all the elements of set A belong to set B. The symbol of the subset is “⊆”.

For example:

A= {1, 2, 3, 4} , B= {1, 2, 3, 4, 5, 6, 7}

A ⊆ B

If A and B are two sets, set B is said to be a subset of set A  if all the elements of set B belong to set A. For example:

A= {a, b, c, d, e, f} , B= {c, d, e, f}

B⊆A

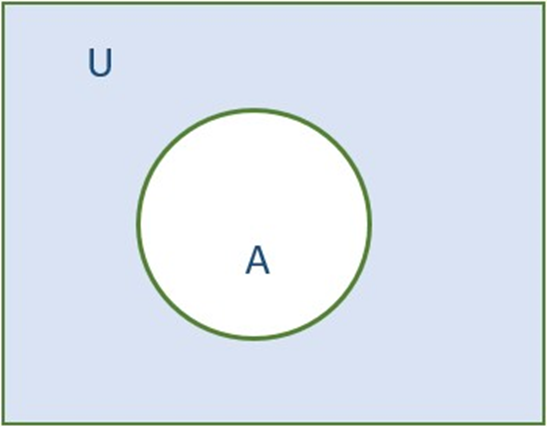
Universal Set

A universal set is a set that has elements of all the related sets without any repetition of elements. A universal set is denoted by U. For example. U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

 A {1, 3, 5, 7, 9} , B= {2, 4, 6, 8}

Frequently Asked Question-FAQs