Quadratic Equation-Formula, Defintion, and Methods to Solve

A quadratic equation is an equation in which the variable has the highest power of two, commonly written as ax²+bx+c=0, Where a, b, and c are real numbers, and a is not equal to 0. Quadratic equations have two possible solutions, also known as roots. These roots can be found using methods such as factorization, completing the square, and the quadratic formula:

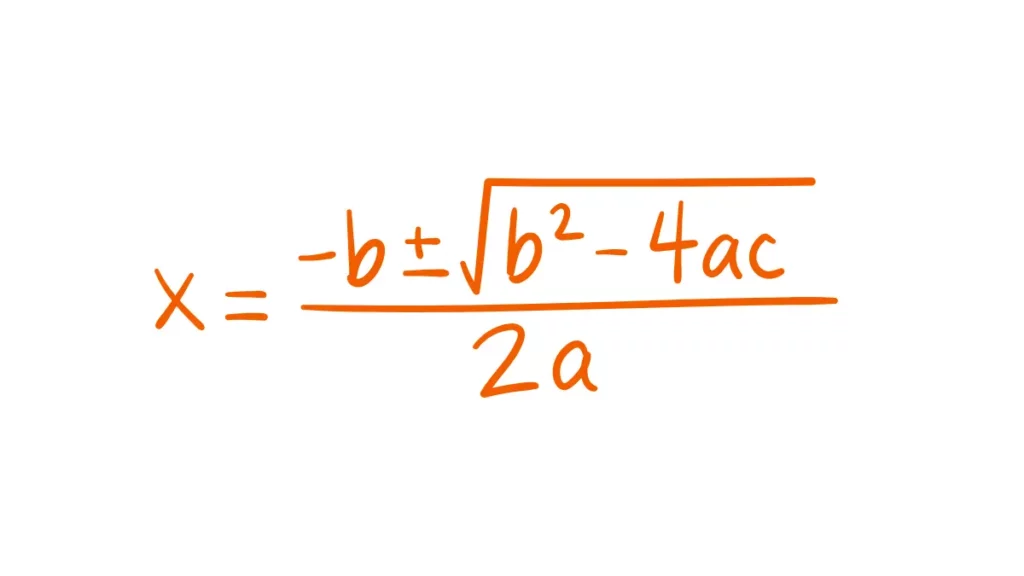
What is a quadratic equation?

A quadratic equation in variable X is an equation in which the greatest exponent of the variable is two.

For example:

                                3x²+4x+2=0        

General form of quadratic equation

                                ax²+bx+c=0

Where a, b, c, ε R and a ≠0 or where a,b,c are real numbers and a≠0

 If a=o

Then bx +c=0 which is not a quadratic equation .it becomes a linear equation.

If b=0

Then ax2+c=0 which is also a quadratic equation. But this is called a pure quadratic equation.

The quadratic equation in its standard form is written as :

ax²+bx+c =0

where:

• a is the coefficient of x²,
• b is the coefficient of x,
• c is the constant term.

The term “quadratic” is derived from “quad,” which refers to the square (because the variable xxx is squared).

Example:

                         2x²+5x+7=0   (general form quadratic equation)

                             3x²+2=0          (   pure quadratic equation)

                                     X+1=0           (linear equation)

Quadratic Formula

The quadratic formula is used to find the roots of a quadratic equation of the form:

How to solve a quadratic equation?

There are three main methods to solve a quadratic equation:

• Factorize
• Completing  the  square 
• Using quadratic formula
• Graphing

What are roots?

Roots are the solutions of a quadratic equation, where the equation equals zero. These roots can vary based on the values of a, b, and c in the equation:

ax²+bx+c =0

Reciprocal Roots

If a=c, one root is the reciprocal of the other.

For example:

2x²+5x+2=0

2x²+4x+x+2=0

2x(x+2) +1(x+2) =0

(2x+1)(x+2)=0

2x+1=0    x+2=0

2x=-1       x=-2

X= -1/2    x=-2

One Root is Zero

If c=0, one of the roots will always be zero.

For example:

2x²+4x=0

2x(x+2) =0

2x=0       x+2=0

X=0           x= -2

Opposite Roots

The roots are equal in magnitude but opposite  in direction (sign) if   b=0

For example:

X²-4=0

X²= 4
square roots on both side

X=±2

X=2      x= -2

Special Sum of Coefficients (a+b+c=0)

If sum of all coefficient is equal to zero. Then 1, c/a are the roots 

For example:

2x²-5x+3=0

2x²-2x-3x+3=0

2x(x-1)-3(x-1) =0

(2x-3)(X-1)=0

2x-3=0      x-1=0

2x=3          x=1

X= 3/2          x=1      

  X=1          x= 3/2

Alternate Coefficient Sum Condition

If  a-b+c =0 than the roots are   -1  , -c/a

For example:

                                                     2x²+5x+3=0

                                                     2x²+2x+3x+3=0

                                                     2x(x+1) +3(x+1) =0

                                                     (2x+3)(x+1)=0

                                                     2x=­­­­­­­-3       x=-1

                                                     X=-3/2        x=-1

• if one root is p+iq  then the second root will be p-iq

• if one root  is p+√q than the second root p- √q

• The quadratic equation whose roots are reciprocal of the roots of    ax²+bx+c=o   is cx²+bx+a=0

Coefficient written is reverse order

For example:

3x²+7x+4=0

3x²+3x+4x+4=0

3x(x+1) +4(x+1) =0

(3x+4)(x+1)=0

3x+4=0     x+1=0

3x=-4        x=-1

X= -4/3         x=-1

For example:

4x²+7x+3=0

4x²+4x+3x+3=0

4x(x+1) +3(x+1) =0

(4x+3)(x+1)=0

4x+3=0       x+1=0

4x=-3           x=-1

X= -3/4            x=-1

• If a=1 and b,c ε z then the roots are rational numbers and must be integers.

For example:

X²+5x+6=0

X²+3x+2x+6=0

X(x+3) +2(x+3) =0

(x+2)(x+3) =0

X+2=0    x+3=0

X=-2       x=-3

• ax² +bx +c=0 

Sum of the roots =S= -b/a

        b=coefficient of x

         a=coefficient of x²

Product of the roots =p=

C=constant

a=coefficient of x²

Frequently Asked Questions-FAQs