Kirchhoff’s Rules | Procedure Of Solution Of Circuit problem

Kirchhoff’s rules describe the electric current of a node and the voltage of a loop. These two laws form the basis of advanced circuit analysis. These laws help in the procedure of solution of circuit problems.

Download the pdf notes of Kirchhoff’s Rules and Procedure Of Solution Of Circuit problem Class 12 Physics

Kirchhoff Current Law

The Sum of all the currents meeting at a point in the electric circuit is zero.

The sum of all the currents flowing towards a point is equal to the sum of all the currents flowing away from the point.

Mathematically

∑I=0

Convention of Current

1) The current flowing towards a point is taken, as positive

2) The current flowing away from a point is taken as negative

Consider four resistances meeting at point A. The current I₁, and I₂ flowing towards point A are taken as +ve and current I₃ and I₄ flowing away from point A is taken as negative.

Mathematically

I₁+I₂+(-I₃)+(-I₄)=0

I₁+I₂=I₃+I₄

Kirchhoff’s point rule

It is also known as Kirchhoff’s point rule which verifies the law of conservation of electric charge. If there is no sink or source of charge at the point, then the total charge flowing towards the point must be equal to the total charge flowing away from the point

Kirchhoff’s Voltage law

 The algebraic sum of voltage changes in a closed circuit or a loop must be equal to zero.

Mathematically

Σν=ο

Consider a closed circuit I is the current which is flowing in the circuit. The direction of the current depends on the cell of a larger EMF.

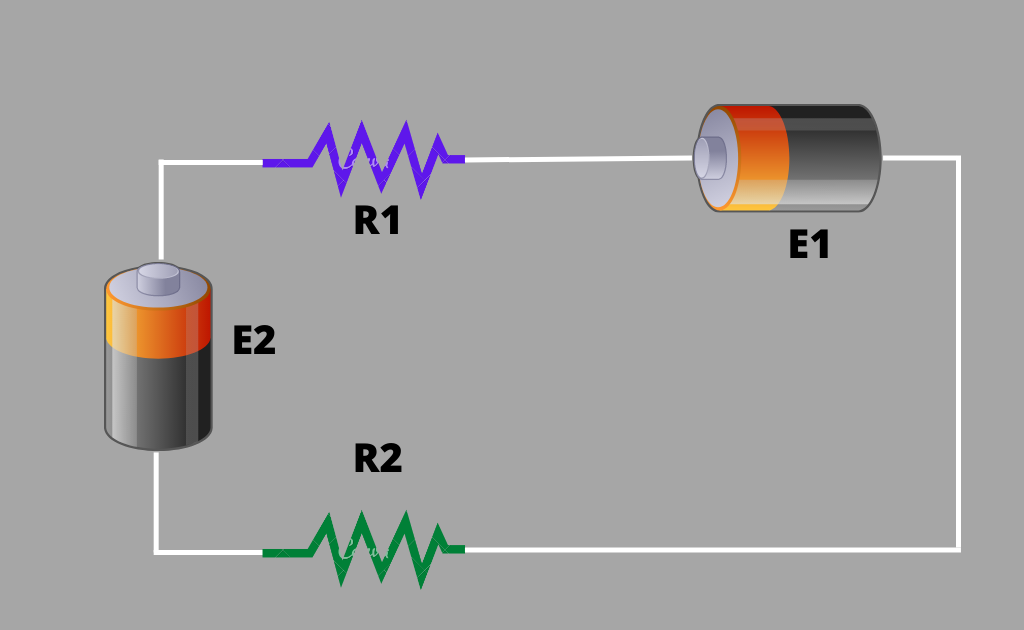
Let E₁> E₂ then the current flows in the anti-clockwise direction. Since the potential difference is equal to the work done on a unit positive charge or it is the gain or loss of energy when the charge is moving from one point to another point.

Thus when a positive charge ΔQ due to the current I in the close circuit is passing through the cell E₁ from low (-ve) to high (+ve) electric potential, work is done on it and it gains energy.

Gain in energy=E₁ΔQ

Similarly, when charge ΔQ passes through the cell E₂ it passes from high to low potential so it loses energy.

 Loss in energy= -E₂ ΔQ

When charge ΔQ passes through resistor R₁ it also loses energy.

 Loss in energy across R₁ = -IR₁ ΔQ      (Since V=IR,)

-ve sign shows that the charge is flowing from high to low potential.

Similarly, the charge also loses energy on passing through the resistor R₂

 Loss in energy across R₂ = – IR₂ ΔQ     

Finally, the charge reaches the negative terminal of cell E₁.

According to the law of conservation of energy, the total change in energy of the system is zero.

E₁ΔQ -E₂ ΔQ -IR₁ ΔQ – IR₂ ΔQ =0

E₁ -E₂ -IR₁ – IR₂ =0

This is Kirchhoff’s second rule and is simply a particular way of stating the law of conservation of energy in electrical problems.

Rules for finding potential changes

• The potential change is +ve if the source of ’emf’ is traversed from the negative to the positive terminal, otherwise, it is negative.
• The potential change is negative if the resistor is traversed in the direction of the current, otherwise, it is positive.

Complex Network

A circuit that consists of many resistors and more than one voltage source is called a Complex Network.

The complex circuit consists of:

Node:

A point where two or more circuit elements

Essential node:

A node where three or more circuit elements join.

Path:

A trace of adjoining basic elements with no elements included more than once

Branch:

The path that connects two nodes

Procedure Of Solution Of Circuit Problems

1) Draw the circuit diagram.

2) The choice of loops should be such that each resistance is included at least once in the selected loop.

3) Assume a loop current in each loop, all the loop currents should be in the same sense. It may be either clockwise or anti-clockwise.

4) Write a loop equation for all the loops.

5) For each loop equation, just follow the rules.

6) Solve these equations for unknown quantities.

Frequently Asked Question-FAQs