Permutation and Combination – Definition, Formulae, and Examples
Permutation and Combination are used for lists (order necessary) or groups( order does not matter).
A permutation is used for lists and Combination is used for groups.
Permutation
An arrangement of a finite number of objects taken some or all at a time is called a permutation. For example the permutation of n different objects taking r (where r ≤ n) at a time is denoted by nPr or P(n,r)
nPr = n!/(n-r)!
Theorem:
nPr = n (n-1)(n-2)…(n-r+1) = n!/(n-r)!
Proof:
Consider we have r places to fill n different objects. First place can be filled-in n different ways. When first place has been filled we are left (n-1) objects. Now second place can be filled in(n-1) different ways. First two places can be filled in n(n-1) ways.
After filling the second place we are left (n-2) different objects. Now third place can be filled in (n-3) different ways. First three places can be filled in n(n-1)(n-2) ways. Proceeding in this way by using fundamental law of counting, total number of arrangements in which r place can be filled up is given by
nPr = n(n-1)(n-2)(n-3)…r factors = n(n-1)(n-1)(n-3)…[n-(r-1)]
nPr = n(n-1)(n-2)(n-3)…(n-r+1)
Multiply and divide R.H.S by (n-r)(n-r-1)…3.2.1
nPr = n(n-1)(n-2)(n-3) x (n-r)(n-r-1)…3.2.1/ (n-r)(n-r-1)…3.2.1
nPr = n(n-1)…(n-r+1)(n-r)(n-r-1)…3.2.1/(n-r)(n-r-1)…3.2.1
nPr = n!/(n-r)!
Examples:
16P4 = 16!/(16-4)! = 16!/12! = 16.15.14.13.12!/12! = 16.15.14.13 = 43,680
14P3 = 14!/(14-3)! = 14!/11!
= 14.13.12.11!/11! = 14.13.12
= 2,184
Permutation with related objects
Theorem:
The number of permutations of n objects taken all at a time when one kind is q alike, the second kind is r alike, and third is s alike is given by
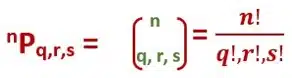
Proof:
Arrangements of q like objects = qPq = q!
Arrangement of s like objects = sPs = s!
Let x be the required number of permutations of n objects
Then total permutations = x. q!r!s!
But a number of permutations of n objects = n!
px. q!r!s! = n! => x = n!/q!r!s!
or
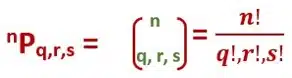
Example:
ASSESSEMENT
S is repeated 4 times
E is repeated 3 times
A,M,N and T come only 1 time.

Combination
When the selection of objects is done neglecting its order, this is called combination.
Combinations of n different objects taken r at a time is denoted by nCr and defines as:
nCr = nPr/r! or nCr = n!/r!(n-r)! nPr = n!/(n-r)!
For r = n nCn = n!/n!(n-n)! = n!/n!0! = 1
For r = 0 nC0 = n!/0!(n-0)! = n!/0!n! = 1
Prove that nCr = n!/r!(n-r)!
Proof
There are nCr combinations of n different objects taken r at a time.
Each combination consists of r different objects which can be permuted among themselves in r! permutation. Total number of permutation of n objects taken r at a time
nCr x r! = nPr => nCr = nPr/r! or nCr = n!/r!(n-r)!
Difference between permutation and combination
- An arrangement where the order is important is called a permutation.
- An arrangement where the order is not important is called combination.
Examples:
10C3 = 10!/3!(10-3)! = 10!/3!7!
= 10.9.8.7!/3.2.1.7! = 120






Leave a Reply