Z-Score-Definition, Calculation, Interpretation, and Examples

A Z-score is also known as a standard score. It is a statistical measurement that describes a value’s relationship to the mean of a group of values. It is measured in terms of standard deviations from the mean.

A Z-score of 0 indicates that the data point’s score is identical to the mean score, while a Z-score of +1.0 indicates a score that is one standard deviation from the mean, and a Z-score of -1.0 indicates a score that is one standard deviation from the mean in the opposite direction.

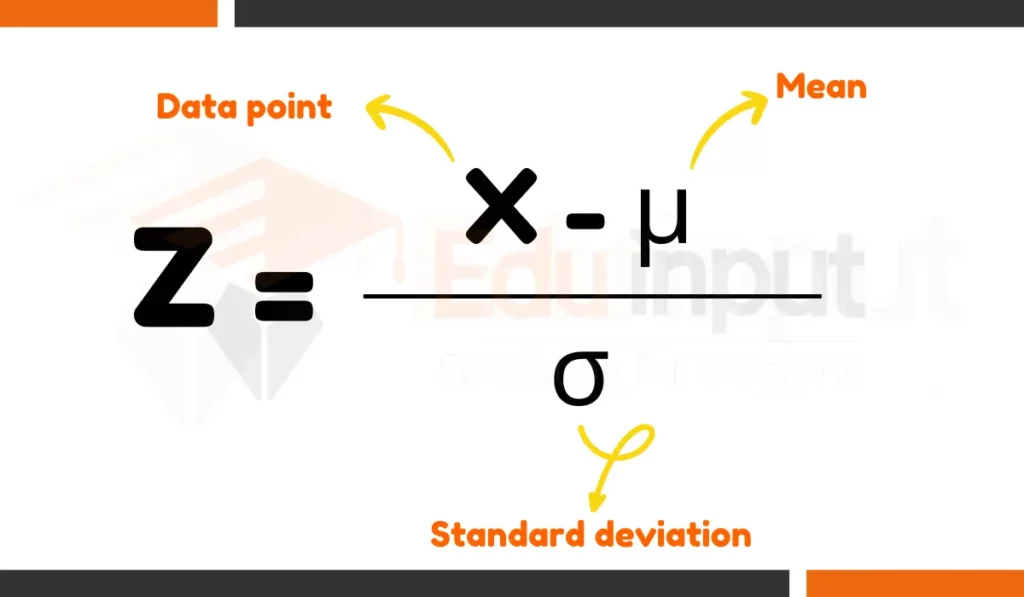
Z-Score Formula

The Z-score formula is given by:

\[ Z = \frac{x – \mu}{\sigma} \]

Where:

• ( Z ) is the Z-score (standard score),
• ( x ) is the observed value,
• ( \mu ) is the mean of the sample, and
• ( \sigma ) is the standard deviation of the sample.

How to Calculate Z-Score?

Here are the steps to calculate z score:

Steps

1. Identify the data point (x): This is the individual value you want to find the z-score for.
2. Identify the mean (μ): This is the average value of the entire data set.
3. Identify the standard deviation (σ): This is a measure of how spread out the data is around the mean.
4. Plug the values into the formula: z = (x – μ) / σ
5. Calculate the z-score: Simplify the expression to get the final z-score.

To calculate a z-score, use formula:

For instance, suppose you scored 75 on a test, the class average is 70, and the standard deviation is 5. The calculation would be:

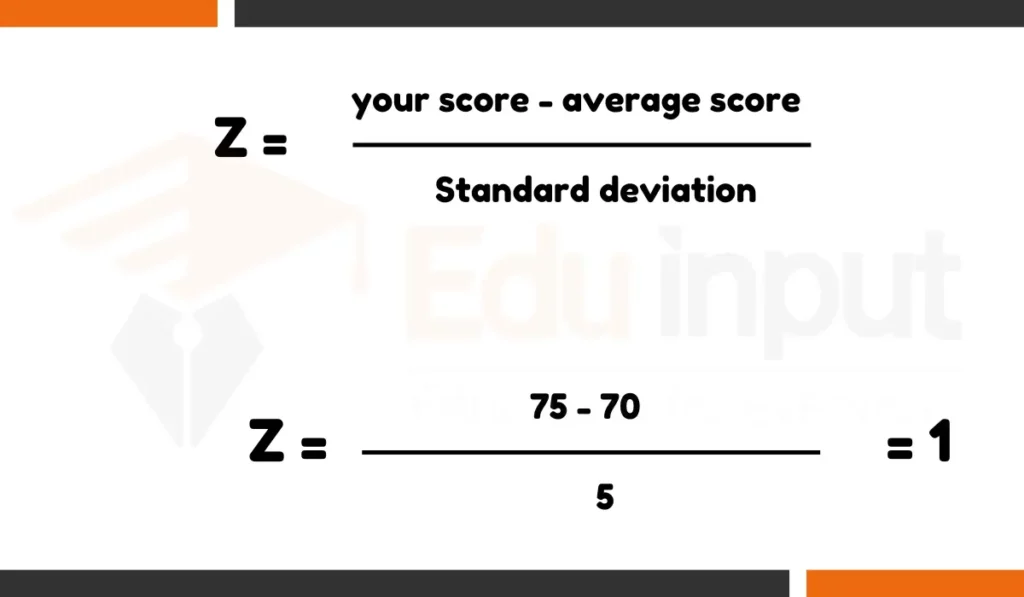
So, your z-score is 1. This means your score is one standard deviation above the average. If the z-score were -1, it would indicate one standard deviation below the average. The z-score helps you understand where your score stands relative to the average and how spread out the scores are.

Z-Score Interpretation

Z-score 0 = mean. Positive z-score = above mean, each unit increase +1 standard deviation. Negative z-score = below mean, each unit decrease -1 standard deviation.

Here is the detailed description to interpret Z-score:

Interpreting value of a z-score:

• 0: A z-score of 0 indicates that the data point is exactly at the mean of the distribution.
• Positive: A positive z-score signifies that the data point is above the mean.
  • The higher the z-score, the further away from the mean and the more unusual the data point is.
  • For example, a z-score of +1 signifies one standard deviation above the mean, while a z-score of +2 signifies two standard deviations above the mean.
• Negative: A negative z-score indicates that the data point is below the mean.
  • The lower the z-score, the further away from the mean and the more unusual the data point is.
  • For example, a z-score of -1 signifies one standard deviation below the mean, while a z-score of -2 signifies two standard deviations below the mean.

Negative and Positive Z-Score Table are given at the end.

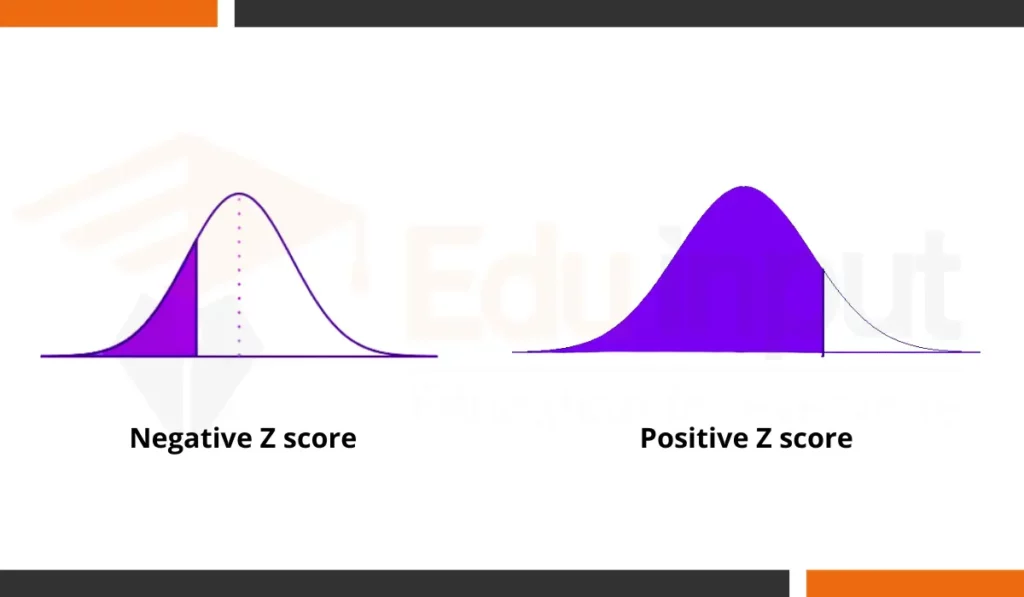
Interpreting z-scores using standard normal distribution

• Area under the curve: The area under the curve of the standard normal distribution represents the probability of a data point falling within a certain range of z-scores.
• Height of the curve: The taller the curve at a particular z-score, the higher the probability of a data point falling within that range.
• Tails of the curve: The tails of the curve represent the less likely z-scores, indicating more unusual data points.

Interpreting z-scores using Standard deviations

• A z-score equal to 1 represents an element, which is 1 standard deviation greater than the mean.
• A z-score equal to 2 signifies 2 standard deviations greater than the mean, etc.
• A z-score equal to -1 represents an element, which is 1 standard deviation less than the mean.
• A z-score equal to -2 signifies 2 standard deviations less than the mean, etc.

Other concepts to Interpret Z-scores

1. Less than 0: A z-score of less than 0 represents an element less than the mean.
2. Greater than 0: A z-score of greater than 0 represents an element greater than the mean.
3. Equal to 0: A z-score of 0 represents an element equal to the mean.
4. Large sets: If the number of elements in the set is large, approximately:

• 68% of the elements have a z-score between -1 and 1.
• 95% have a z-score between -2 and 2.
• 99% have a z-score between -3 and 3.

Understand Z-scores with Real-world Examples

Z-scores help us understand how individual data points relate to the overall average and spread of a dataset. They are especially useful when comparing data sets with different units or scales. Here are some real-world examples:

Example 1: Exam Scores

Imagine a student scored 75 points on a math exam with an average score of 70 and a standard deviation of 5. To compare their score with the class performance, we calculate the z-score:

                    
                       z = (75 - 70) / 5 = 1

A z-score of 1 indicates the student scored 1 standard deviation above the average.

Example 2: Plant Heights

Suppose you measure the height of sunflower plants in your garden. You find their average height is 20 inches with a standard deviation of 2 inches. One sunflower stands out at 24 inches tall. We can calculate its z-score:

             z = (24 - 20) / 2 = 2

A z-score of 2 signifies this sunflower is 2 standard deviations taller than the average plant, indicating a potentially significant difference.

Example 3: Stock Prices

Assume you’re analyzing stock market data. The average stock price for a certain company is $100 with a standard deviation of $10. You observe a price of $115 for a specific stock. Calculating the z-score gives:

                    
                  z = (115 - 100) / 10 = 1.5

A z-score of 1.5 suggests the stock price is 1.5 standard deviations higher than the average, potentially indicating a period of growth or increased interest.

Z-Scores and Their Corresponding Probabilities/Percentiles:

1. Z-score 0.05: Approximately 1.645 standard deviations below the mean (84.134% probability)
2. Z-score 0.025: Approximately 1.960 standard deviations below the mean (97.5% probability)
3. Z-score 0.5: Mean (50% probability)
4. Z-score 0: Mean (50% probability)
5. Z-score 0.01: Approximately 2.326 standard deviations above the mean (98.764% probability)
6. Z-score 0.005: Approximately 2.576 standard deviations above the mean (99.379% probability)
7. Z-score 0.95: Approximately 1.645 standard deviations above the mean (84.134% probability)
8. Z-score 0.1: Approximately 1.282 standard deviations below the mean (89.442% probability)
9. Z-score 0.25: Approximately 0.675 standard deviations below the mean (77.337% probability)

Z-Scores and Percentiles

1. Z-score 1: Approximately 84th percentile
2. Z-score 1.5: Approximately 93rd percentile
3. Z-score 1: 84th percentile
4. Z-score 1.28: Approximately 89th percentile
5. Z-score 1.96: Approximately 97.5th percentile
6. Z-score 1: Approximately 84th percentile
7. Z-score 1.25: Approximately 89th percentile
8. Z-score -1.28: 10th percentile
9. Z-score 1.2: Approximately 88th percentile
10. Z-score -1.28: 10th percentile

Negative Z-Score Table

Z-Score	Probability
-3.0	0.0013
-2.9	0.0019
-2.8	0.0026
-2.7	0.0035
-2.6	0.0047
-2.5	0.0062
-2.4	0.0082
-2.3	0.0107
-2.2	0.0139
-2.1	0.0179
-2.0	0.0228
-1.9	0.0287
-1.8	0.0359
-1.7	0.0446
-1.6	0.0548
-1.5	0.0668
-1.4	0.0808
-1.3	0.0968
-1.2	0.1151
-1.1	0.1357
-1.0	0.1587
-0.9	0.1841
-0.8	0.2119
-0.7	0.2420
-0.6	0.2743
-0.5	0.3085
-0.4	0.3446
-0.3	0.3821
-0.2	0.4207
-0.1	0.4602
-0.09	0.4681
-0.08	0.4761
-0.07	0.4840
-0.06	0.4920
-0.05	0.5000
-0.04	0.5080
-0.03	0.5160
-0.02	0.5240
-0.01	0.5320
-0.009	0.5331
-0.008	0.5341
-0.007	0.5351
-0.006	0.5361
-0.005	0.5371
-0.004	0.5381
-0.003	0.5391
-0.002	0.5401
-0.001	0.5411
-0.000	0.5413

Positive Z-Score Table

Z-Score	Probability
0.000	0.5413
0.001	0.5423
0.002	0.5433
0.003	0.5443
0.004	0.5453
0.005	0.5463
0.006	0.5473
0.007	0.5483
0.008	0.5493
0.009	0.5503
0.01	0.5513
0.02	0.5591
0.03	0.5669
0.04	0.5747
0.05	0.5826
0.06	0.5904
0.07	0.5982
0.08	0.6061