Probability Mean in Math|Types of Probability

Probability is an important concept in mathematics and statistics that deals with the likelihood or chance of an event occurring. It is used in a wide range of fields, from science and engineering to finance and economics. In this article, we will discuss what probability is, how it is calculated, and its applications.

Introduction

Probability is a branch of mathematics that deals with the study of uncertainty. It involves the measurement of the likelihood of an event occurring. Probability theory is used in various fields, including science, engineering, finance, economics, and gaming.

The concept of probability can be difficult to understand at first. However, with the right approach, anyone can learn to calculate and use probabilities in practical situations.

What is Probability?

Probability is the measure of the likelihood of an event occurring. It is expressed as a number between 0 and 1, where 0 represents an impossible event, and 1 represents a certain event. Probability is denoted by the symbol P.

Probability Terms

To understand probability, it is essential to know some of the terms used in probability theory. The following are some of the commonly used probability terms:

Experiment: An experiment is any process that can produce one or more outcomes.

Outcome: An outcome is the result of an experiment.

Sample Space: The sample space is the set of all possible outcomes of an experiment.

Event: An event is a subset of the sample space.

Probability Space: A probability space is a sample space along with a probability function that assigns a probability to each event.

Types of Probability

There are three types of probability:

Classical Probability

Empirical Probability

Subjective Probability

Classical probability is used when the outcomes of an experiment are equally likely. Empirical probability is based on observations and experiments. Subjective probability is based on personal judgments and opinions.

Probability Calculations

Combinatorics

Combinatorics is the branch of mathematics that deals with the study of counting and arranging objects. It is an essential part of probability theory.

There are two types of combinatorial problems:

Permutations

Combinations

Permutations deal with the number of ways in which objects can be arranged in a particular order. Combinations deal with the number of ways in which objects can be selected without regard to order.

Probability Laws

Probability laws are used to calculate the probability of an event occurring. The three main probability laws are:

Addition Rule

Multiplication Rule

Law of Total Probability

The addition rule is used to calculate the probability of two or more events occurring. The multiplication rule is used to calculate the probability of two or more independent events occurring. The law of total probability is used to calculate the probability of an event occurring when there are several possible ways in which it can occur.

Conditional Probability

Conditional probability is the probability of an event occurring given that another event has already occurred. It is denoted by P(A|B), which is the probability of A given B.

Conditional probability is essential in many practical situations, such as medical diagnosis and weather forecasting.

Probability Distributions

Probability distributions are used to describe the probability of different outcomes in an experiment. There are two types of probability distributions:

Discrete Probability Distributions

A discrete probability distribution is used when the possible outcomes of an experiment can be counted, such as the number of heads when tossing a coin.

The two most common types of discrete probability distributions are the binomial distribution and the Poisson distribution.

Continuous Probability Distributions

A continuous probability distribution is used when the possible outcomes of an experiment cannot be counted, such as the height of people in a population.

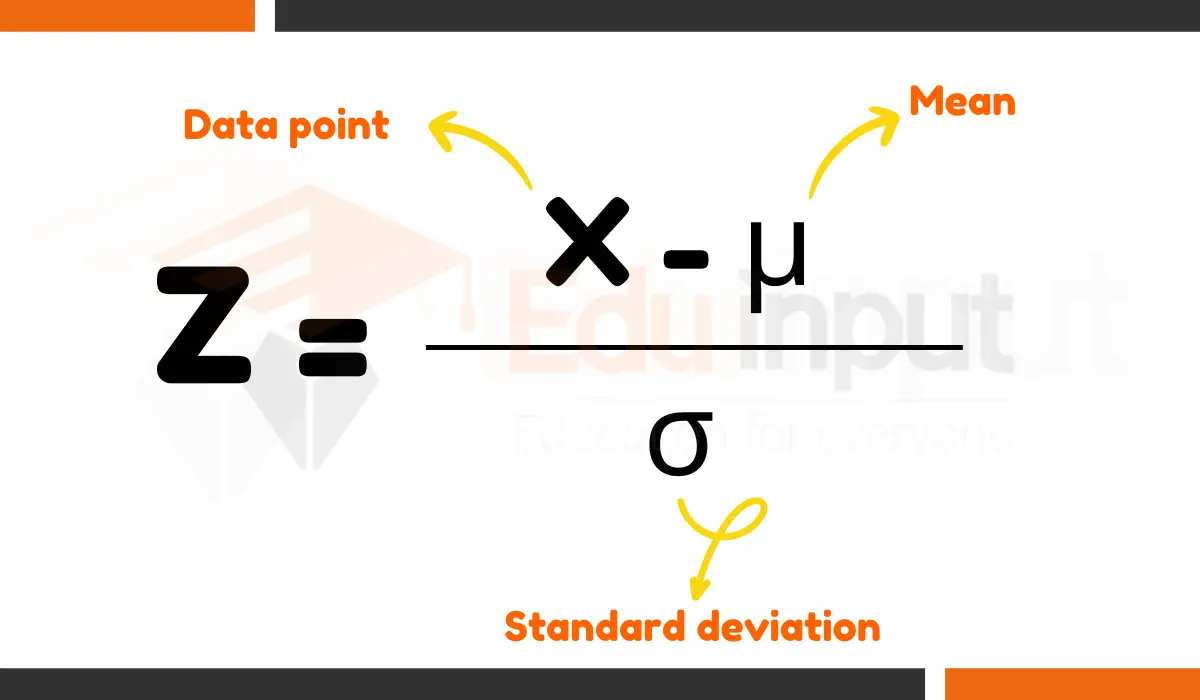
The most common type of continuous probability distribution is the normal distribution.

Applications of Probability

Probability has a wide range of applications in different fields. Here are some examples:

In Science and Engineering

Probability is used in science and engineering to model and predict the behavior of physical systems. It is used in fields such as physics, chemistry, and engineering to study phenomena such as the behavior of particles, the reliability of systems, and the likelihood of accidents.

In Finance and Economics

Probability is used in finance and economics to model and predict the behavior of financial markets and economic systems. It is used in fields such as investment banking, risk management, and insurance to study phenomena such as the behavior of stock prices, the likelihood of defaults, and the risk of financial loss.

In Gaming and Gambling

Probability is used in gaming and gambling to calculate the odds of winning and losing. It is used in fields such as casinos, lotteries, and sports betting to study phenomena such as the behavior of players, the likelihood of winning, and the risk of loss.

Summary

Probability is a crucial idea in both mathematics and statistics, concerned with measuring the probability or possibility of a particular event taking place. This concept has many practical applications across various disciplines, including science, engineering, finance, and economics. A solid grasp of probability is necessary for making well-informed decisions and accurate predictions.