Relation Between Angular And Linear Velocities

In this article, we will discuss the relation between angular and linear velocities. The rate of change of angular displacement is called angular velocity. And the rate of change of linear displacement is called linear velocity.

Consider a rigid body rotating about the z-axis with an angular velocity ω along a circle of radius ‘r’. Point P moves along a circle with a linear velocity V but the line OP rotates with angular velocity ω.

As the axis of rotation is fixed, the direction of ω remains the same and so can be considered as a scalar. Similarly, we only considered the magnitude of linear velocity which is also treated as a scalar.

Download pdf notes of Relation between Angular and Linear Velocities class 11 physics

Relation Between Angular And Linear Velocities

Consider the motion of point P along the circle. Let point P moves through distance P₁P₂ = Δs in time interval Δt. Then the reference line OP has an angular displacement Δθ radian in that time interval Δt.

Then by the relation

Δs=r Δθ

Dividing the both sides by Δt and applying limit Δt -0

lim_Δt–0 Δs/ Δt = r lim_Δt–0 Δθ/ Δt

V=rω

This equation shows the relation between angular and linear velocities. Where v is the velocity of point P and ω is the angular velocity of reference line OP.

In the limit, Δt–0 the length of arc P₁P₂ becomes very small and its direction is tangent to the circle at point P_1.

Thus the magnitude of velocity when moving along the circle is V but its direction is tangent to the circle. That is why the linear velocity of point P is also known as tangential velocity.

Difference Between Angular And Linear Velocity

Angular velocity	Linear Velocity
The rate of change of angular displacement is called angular velocity	The rate of change of linear displacement is called linear velocity
In a circular motion, the angular velocity of a particle is along the axis of a circle.	In a circular motion, the linear velocity of a particle is along the circumference of a circle.
Angular velocity remains the same in a circle.	Linear velocity changes at every point in the circle.
The Units of Angular velocity are degree and radian.	The Unit of linear velocity is m/s.
Angular velocity is represented by ω	Linear velocity is represented by v

Relation between Linear and Angular Acceleration

When the reference line OP is rotating with an angular acceleration α the point P will also have a linear or tangential acceleration α.

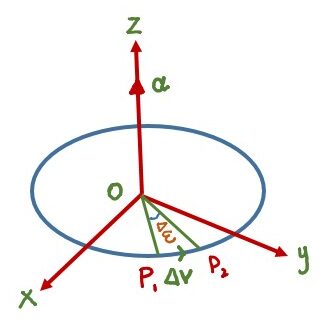
Let the change in linear velocity is Δv and the change in angular velocity be Δω in time interval Δt when the body is rotating along a circle.

Thus

Δv=rΔω

Dividing by Δt and applying the limit lim_Δt–0 we have

lim_Δt–0Δv/Δt = r lim_Δt–0Δω/Δt

a_t = rα

From equations of the relation between angular and linear velocities v = rω and a_t = rα it is clear that for a rotating body the points at different distances from the axis of rotation do not have the same speed or acceleration. But all points have the same angular displacement, angular speed, and angular accelerations.

Equations of Angular Motion

Linear(a = constant)	Angular(α = constant)
Vf=vi+at	ωf=ωi+αt
S=vit+1/2gt2	θ=ωit+1/2αt2
2as=vf2-vi2	2α θ= ωf2 – ωi2

The equations of angular motion are exactly the same as those in linear motion except that θ, ω, and α are replaced by s, v, and a respectively.

These angular equations of motion are only valid for fixed axes of rotation and constant angular acceleration. Since all angular vectors have the same direction, so they can be considered scalars.

Related FAQs