Angular Momentum | Law of Conservation of Angular Momentum

Angular momentum is defined as a particle that is said to possess an angular momentum about a reference axis if it so moves that its angular position changes relative to that reference axis.

Angular Momentum

The cross product of position vector r concerning the axis of rotation and linear momentum P of an object is called angular momentum.

Angular Momentum Formula

L=rxP

Where L is angular momentum. r is the position vector and P is representing the linear momentum.

Relation between angular and linear momentum

Consider a particle of mass ‘m’ moving with velocity v having momentum P relative to the origin O, then its angular momentum is given by

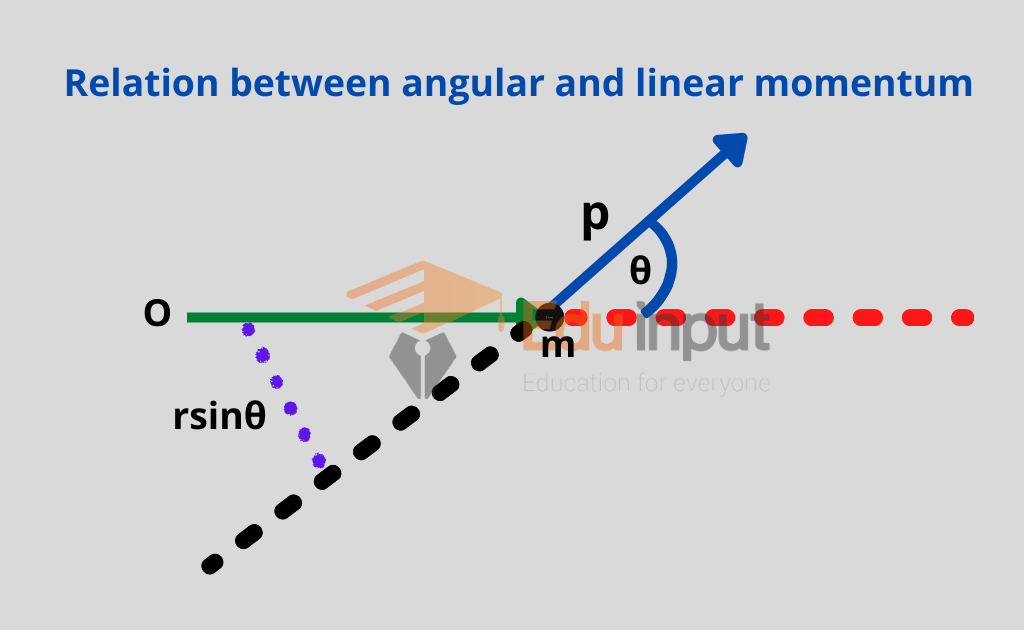
L=rxP where r is the position vector

L=rpsinθn=rpsinθ

But P=mv

L=mrvsinθ

If the particle is moving in a circle of radius ‘r’ with uniform angular velocity ‘ ω’ then the angle between ‘r and tangential (linear) velocity is 90

L=mrvsinθ=mrv sin90=mrv

But according to the relation between angular and linear velocity

V=rω

L=mr (r ω) = mr² ω

The direction of Angular Momentum

Angular momentum is a vector quantity. Its direction is determined by the right-hand rule. Angular momentum L is perpendicular to the plane containing r and P.

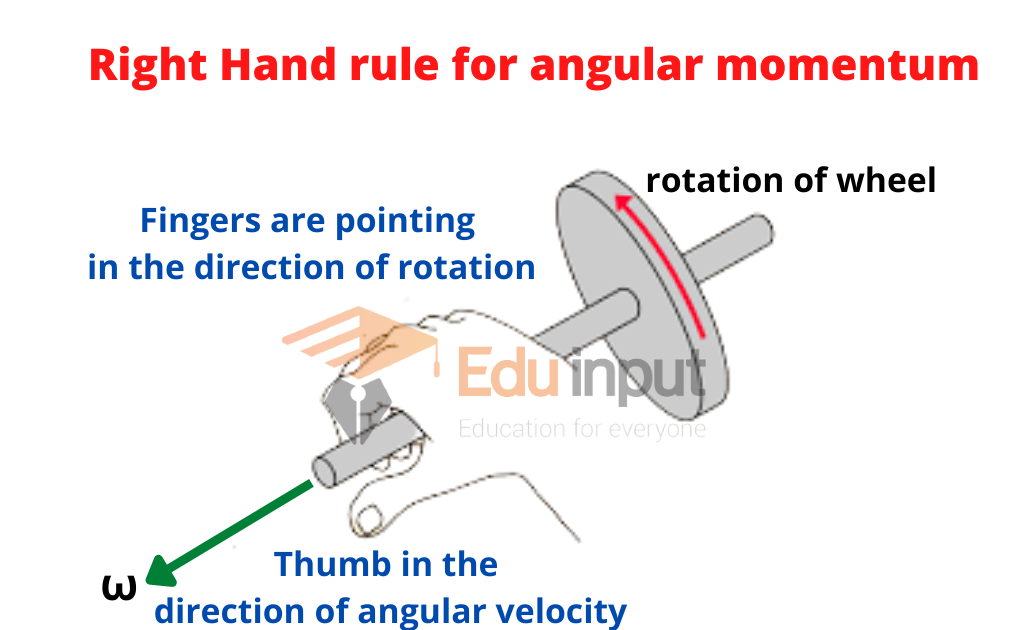
Angular momentum has an important role in the study of rotational motion.

Angular Momentum Units

SI unit of angular momentum is kgm²/s. J/s is also a unit of angular momentum. The dimension of angular momentum is [ML² T^-1]

Angular momentum of Rigid Body:

If the distance between the particles doesn’t change on applying force then the body is said to be a rigid body.

Consider a symmetric rigid body rotating about a fixed axis through the center of mass. Each particle of the rigid body rotates about the same axis in a circle with the same angular velocity ‘ ω ‘.

The magnitude of the angular momentum of the particle of mass m_i about origin O is m_iv_ir_i.

The direction of L_i is the same as that of ω so

Angular momentum of an ith particle is v_i=r_iω_i

The total angular momentum of all particles of a rigid body is

L= (Σ m_ir _i²) ω =lω

Where I is the moment of inertia of the rigid body about the axis of rotation.

Spin Angular Momentum:

The angular momentum of a spinning body is called spin angular momentum. It is denoted by L_s.

Example: Spinning top.

Orbital Angular Momentum:

The angular momentum associated with the motion of a body along a circular path is called orbital angular momentum. It is denoted by L_a.

Example: earth revolving around the sun

Point Object:

If the orbital radius is large as compared to the size of the body, the body is considered to be a point object.

Law of conservation of angular momentum:

If no external torque acts on a system, the total angular momentum of the system remains constant.

Mathematically

L_total=L₁+L₂+….=constant

This law is one of the fundamental principles of physic.

The diver pushes off the board with a small angular velocity about a horizontal axis through his center of gravity G.

When he leaves the board, his legs and arms are fully extended. The diver has a large moment of inertia I about this axis due to the large value of r.

 Angular velocities are small. When the diver curls his body, the moment of inertia reduces to I2 due to the small value of r. To conserve the angular momentum the value of angular velocity increases to ω₂

L=I₁ω₁=I₂ ω₂=Constant

In this way, he can make more somersaults before entering the water.

The angular momentum is a vector quantity. Its direction is along the axis of rotation. Thus the direction (orientation) of the axis of rotation cannot be changed without the effect of any external torque.

This fact has great importance for Earth’s motion around the Sun. No other considerable torque is experienced by the Earth because the major force acting on it is the pull of the Sun.

 The Earth’s axis of rotation, therefore, remains fixed in one direction concerning the universe around us.

Application of Law of Conservation of Angular Momentum

• Ice skaters
• Ballet dancers make use of this law to show spectacular feats

Related FAQs