Rotational Kinetic Energy | Rotational Kinetic Energy of Disc and Hoop

The energy of an object due to its rotation about an axis is called rotational kinetic energy.

Rotational kinetic energy

 The energy of an object due to spinning about an axis is called rotational kinetic energy. Rotational kinetic energy is directly proportional to the rotational inertia and the square of the magnitude of the angular velocity.

Rotational kinetic energy formula

Consider an object spinning about an axis with constant angular velocity ω. Every point of the body has some K.E due to circular motion.  In order to calculate the total K.E of the spinning body, imagine that it is composed of tiny pieces of masses m₁, m₂…. ..,m_n,.

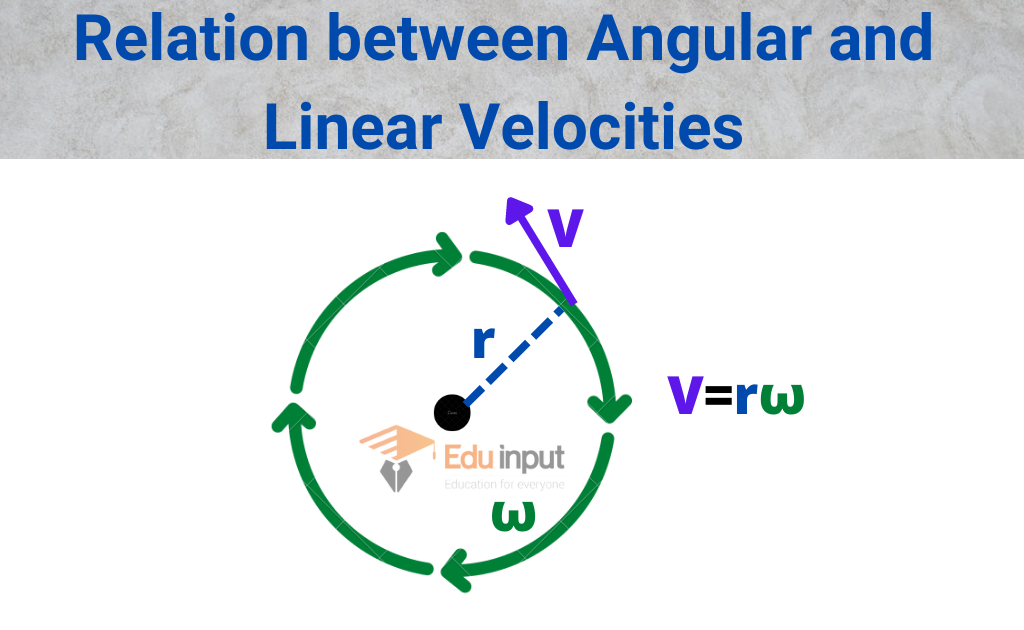
Consider a single piece of mass m_i, at a distance r_i from the axis of rotation moving in a circle. Then its speed is given by

V_i= r_iω

K.E= 1/2m_iv_i²

=1/2m_i (r_iω)²  =1/2m_Ir_i²ω²

The rotational K.E of the whole body is the sum of the kinetic energies of all the pieces.

K.E_rot = 1/2 m_ir_i²ω² +1/2m₂r₂²ω² +1/2m³r₃²ω²

=1/2(m₁r₁²+ m₂r₂²+………. ) ω²

I= m₁r₁² +m₂r₂²+……

Rotational kinetic energy uses

Rotational K.E is practically used by flywheels, which are essential parts of many engines. Flywheel stores energy between powers stokes of the piston which is distributed over the full revolution of the crankshaft and rotation remains smooth.

Rotational Kinetic Energy of Disc and Hoop

Consider a disc and a hoop started moving down on an inclined plane of height ‘h’. They have rotational as well as translational motion. If there is no friction, then the total K.E of the disc or hoop on reaching the bottom of the inclined plane must be equal to its P.E at the top.

P.E _{at top} = Rotational K.E _{at bottom} + Translational K.E _{at bottom}

Rotational Kinetic Energy of Disc

P.E = K.E_rot +K.E_tran

K.E_rot=1/2lω²

K.E_rot=1/2 (1/2mr²ω²)

=1/4mr²ω²

=1/4mv²

P.E=1/4mv² +1/2mv²

mgh=mv²+2mv²/4

mgh=3/4mv²

v²= 3/4gh

v=√3/4gh

Rotational Kinetic Energy of hoop

P.E = K.E_rot +K.E_tran

K.E_rot=1/2lω²

K.E_rot=1/2mr²ω²

=1/2mv²

mgh= mv²+mv²/2

mgh =2 mv²/2

v²=gh

v=√gh

This is the final velocity of a hoop on reaching the lower end of an inclined plane. It shows that the velocity of the disc will be greater than the hoop on reaching the bottom of the inclined plane.