Bohr’s Atomic Model-Postulates and Mathematically derived equation

Introduction to Bohr’s atomic model

In 1887, the spectra of hydrogen were recorded by Lyman and Balmer. The lines of the spectra could not be explained. Moreover, the defective Atomic model of Rutherford also needed correction. In the light of all these shortcomings, Bohr gave his own model of the atom in 1913.

Postulates of Bohr atomic model

The following are the postulates of Bohr’s model of the atom:

1. The electrons revolve around the nucleus in a circular manner.

2. As long as an electron remains in a particular orbit, it neither loses the energy nor gains the energy. Thus in a particular orbit, the energy of the revolving electron remains constant. Such energy levels are called stationary energy levels.

When the electron jumps from a lower energy level to a higher energy level it absorbs the energy in the form of a photon. When the electron jumps from a higher energy level to a lower one, it loses energy in the form of a photon.

So

                     ΔE = hv

Where, ΔE is the energy difference between the levels h is Planck’s constant and the value is 6.02 x 10-34Js γ is the frequency of the photon emitted or absorbed.

The electron can move only in that orbit in which the angular momentum of the electron (mvr) is an integral multiple of h/2π 

   So,           mvr = nh/2π 

Where

‘n’ is a simple integer and is the number of orbits in other worlds the angular momentum is quantized.

The values of angular momentum for the first four orbits are

   h/2π, 2h/2π, 3h/2π, 4h/2π 

Also read: What is an atomic model in chemistry?

MATHEMATICAL DERIVATION OF BOHR’S RADIUS

Consider an atom having one electron. The charge of the nucleus is Ze⁺. The electron of mass ‘m’ is moving in a circular manner with the radius ‘r’ with velocity ‘v’

The number of photons is Z and e⁺ is the charge of a photon.

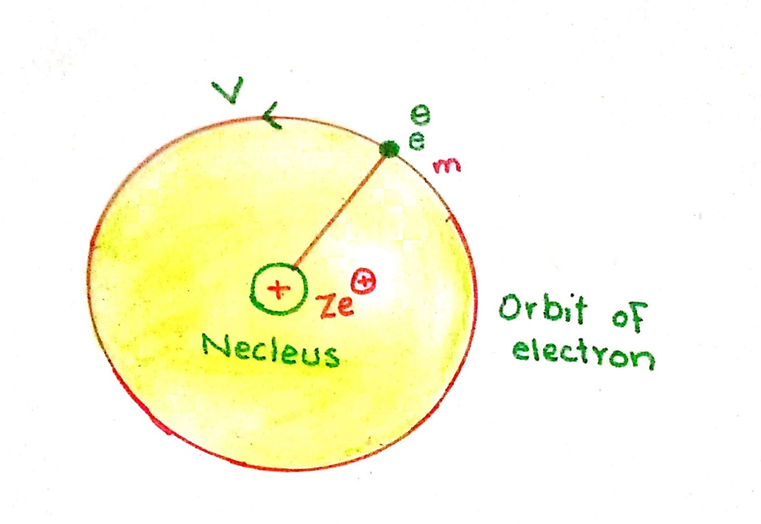
The force with which the electron wants to fly away is the centripetal force

           F = mv²/r

The force is balanced by the electrostatic force of attraction of the electron (Ze⁺) and the nucleus (Ze⁺). According to coulombs law, the force of attraction is

     F = Ze⁺. e^– /4π ∈_or²

  Here ∈0 (epsilon) is a proportionally constant. It is known as the permittivity of the vacuum. Its numerical value is

                          ∈0 = 8.854 x 10^-12C²J^-1m-1

The electron can only revolve in orbit if the centripetal force and the coulombic are equal.

            mv² /r = Ze²/4π ∈_or²

                      mv^{2 =} Ze²/4π ∈_or

                            r = Ze²/ 4π ∈_or²

According to equation (5), the radius of the atom is inversely proportional to the electron. It means that when the electron goes to the higher orbits its velocity decreases.

But the determination of the velocity of the revolving electrons in a very small-sized atom is impossible. So we eliminate the factor of velocity from equation (5). For this purpose, we take the help of the fourth postulate of Bohr’s model.

                                 Mvr = nh /4π

                      V = nh/2πmr

Taking Square,

                        V² = n²h²/4π²m²r² ———— (6)

Putting equation (6) into equation (5)

                   r = Ze²/4∈_o m x n²h²/4π²m²r²

Simplifying this equation, taking r on L.H.S. and other factors on right R.H.S.

            r =   n²h²∈_o / πmZe² ———– (7)

             e = h² ∈_o/πme² (n²/Z) ———– (8)

Actually, we have re- arranged the equation (7) and the constant factors have been taken outsides the brackets. If we do the calculations of these factors, by putting their values as,

               h = 6.625 x 10^-34Js, ∈_o = 8.854 x 10^-12 C J^-1 m^-1

                          π = 3.1416, m = 9.106 x 10^-31 kg,

                 e^– = 1.602 x 10^-19 C

       Then, h²∈_o/ πme2 = 0.529 x 10^-10m

‘m ’is the unit of length

 Since, 10^-10 m = 1A^o so equation (8) becomes

            r = 0.529 (n²/z) A^o

^{This equation (9) is for any atomic system having one electron, and revolving around Z-protons.}

^{Let us apply this equation on the hydrogen atom for which}

 ^{Z = 1(H atom has one proton in the nucleus)}

                r = 0.529(n²) A^o

With the help equation (10) let us calculate the radii of first five orbits of hydrogen atom

    r₁ = 0.529A^o (1²)= 0. 529A^o

      r₂ = 0.529A^o (2²) = 2.41A^o

    r₃ = 0.529A^o (3²) = 4.8A^o

    r₄ = 0.529A^o (4²) = 8.4A^o

  r₅ = 0.529A^o (5²) = 13.2A^o

These calculations show that distances between adjacent orbits go on increasing from the lower to higher ones.

These calculations tell us that the second orbit is four times more away than the first one from the nucleus. The third orbit is nine times away. In other words, the atom becomes thinner as one goes away from the nucleus.