Geometric Interpretation of Vector

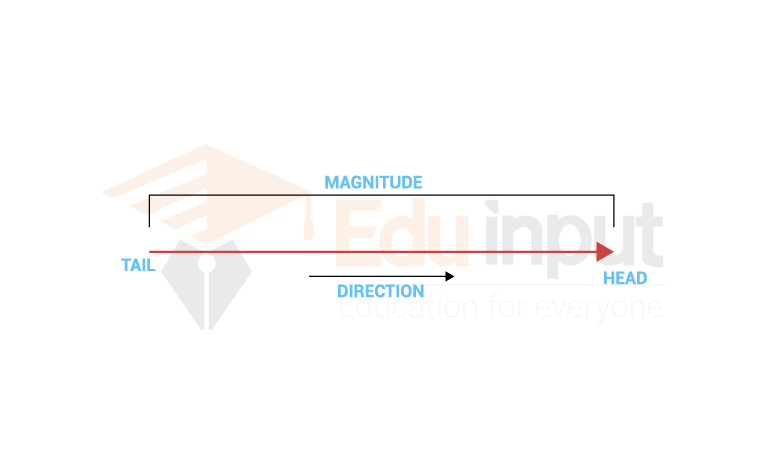
Vectors can be denoted geometrically by arrows (directed line segments). The arrowhead represents the direction of the vector, and the length of the arrow explains the magnitude of the vector. →PQ,v,or→v. We often write v=→PQ

Geometric interpretation of vector

Geometrically, a vector is denoted by a directed line segment AB with A its initial point and B its terminal point. It is often found convenient to represent a vector by an arrow and is written either as a line on the head of AB or as a boldface symbol like v or in underlined form v

• The magnitude or length or norm of a vector AB or v is its absolute value and is written as| AB| or simply AB or| v_–|

• A unit vector is defined as a vector whose magnitude is unity. The unit vector of vector v_– is written as v^{^}_– (read as v_– hat) and is defined by

• If terminal point B of a vector^àAB coincides with its initial pints A, then magnitude AB=0 and

AB=0, which is called zero or null vectors

• Two vectors are said to be negative on each other if they have the same magnitude but in the opposite direction.