Prime Factorization with Prime Factor Trees

Prime factorization is a fundamental concept in mathematics that allows us to break down a number into its prime factors.

In this article, we will explore prime factorization using a visual tool called “Prime Factor Trees.”

What is Prime Factorization?

Prime factorization is the process of expressing a number as the product of its prime factors. Prime factors are the building blocks of all numbers.

How to Create a Prime Factor Tree

Creating a prime factor tree is a visual way to find the prime factors of a number. Here’s how you can do it:

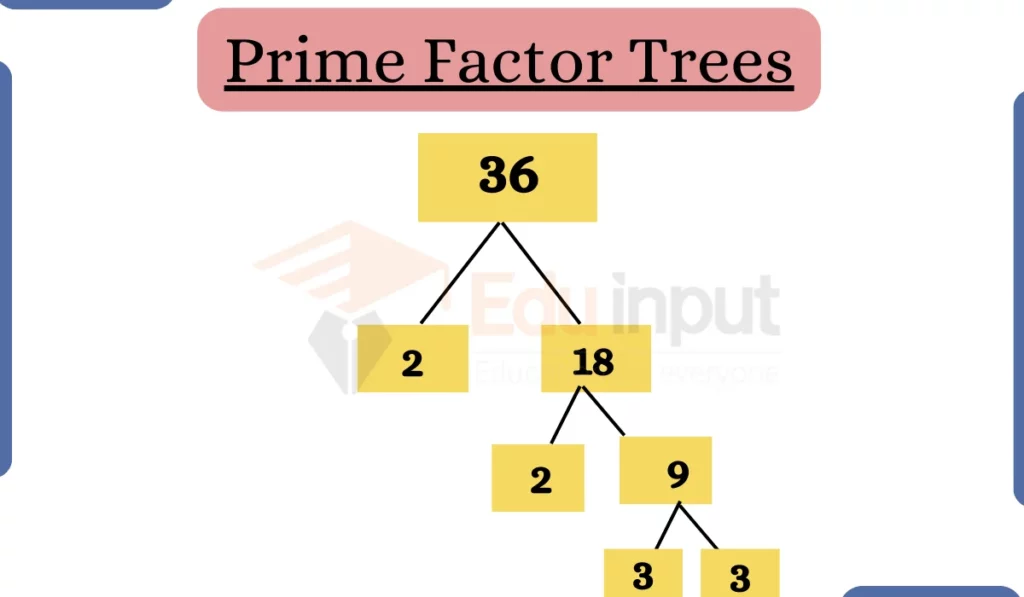
• Start with a Number: Begin with the number you want to factorize. For example, let’s take the number 36.
• Find Two Factors: Identify two numbers that multiply to give you the original number. In our example, 36 can be divided into 6 and 6, which are 2 x 18.
• Continue Factoring: Repeat this process for each factor until you can no longer divide. For 18, you can split it into 2 and 9, which are 2 x 3 x 3.
• Draw the Tree: Create a tree-like diagram with branches for each factorization step. It should look like this:

Solved Examples

Example 1

Prime Factorization of 48

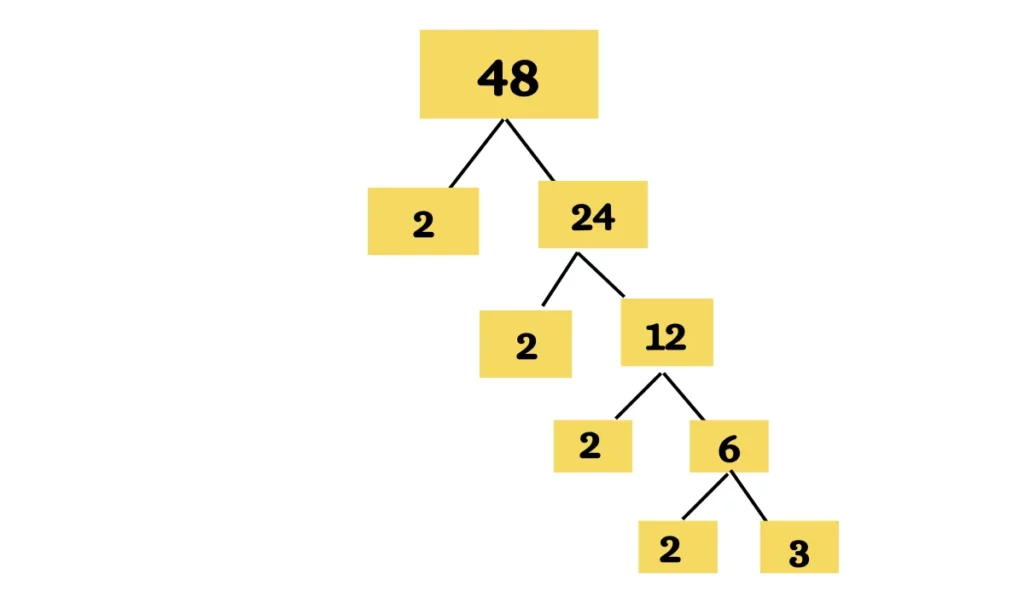
• Start with 48.
• Divide it into 2 and 24 (2 x 24).
• Continue factoring 24 into 2 and 12 (2 x 12).
• Further factor 12 into 2 and 6 (2 x 6).
• Finally, 6 can be split into 2 and 3 (2 x 3).

So, the prime factors of 48 are 2 x 2 x 2 x 2 x 3.

Example 2

Prime Factorization of 90

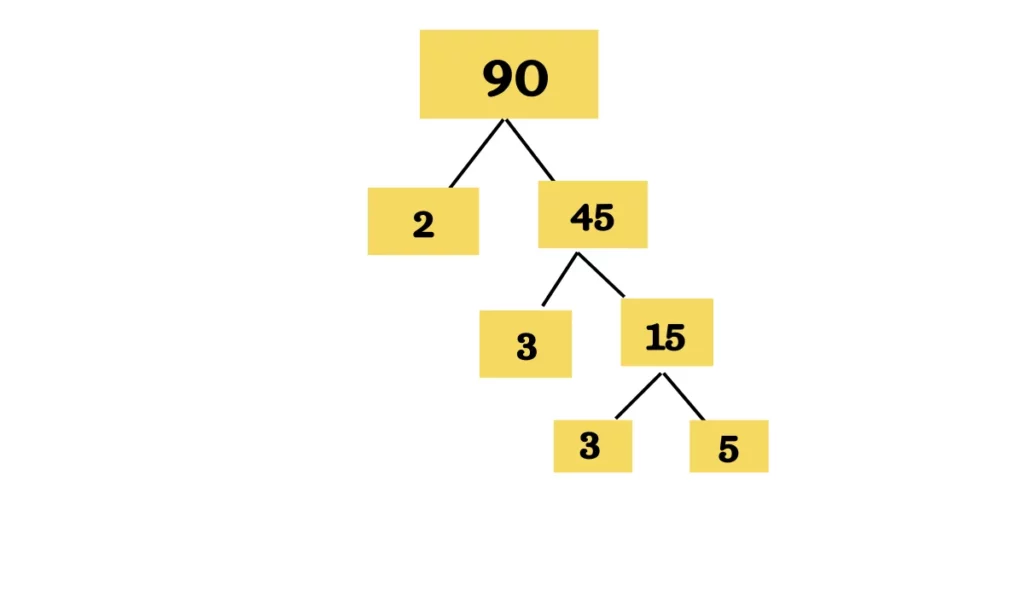
• Start with 90.
• Divide it into 2 and 45 (2 x 45).
• Continue factoring 45 into 3 and 15 (3 x 15).
• Further factor 15 into 3 and 5 (3 x 5).

The prime factors of 90 are 2 x 3 x 3 x 5.

FAQs